4.2 Transformaciones en 3D

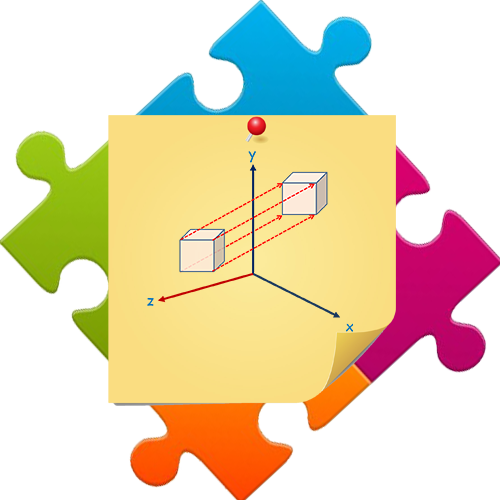
Los métodos para las transformaciones geométricas en tres dimensiones se extienden  de los métodos bidimensionales al incluir las consideraciones para la coordenada de z.

Traslación

Se traslada un objeto al especificar un vector de traslación tridimensional, que determina el desplazamiento del objeto en cada una de las tres direcciones de las coordenadas.

En la representación homogénea tridimensional de las coordenadas, se traslada un punto de la posición P=(x,y,z) a la posición P’=(x,y,z) con la operación de matriz:

A los parámetros t_x, t_y, t_z que especifican las distancias de traslación para las direcciones de las coordenadas x,y y z, se asignan cualesquiera valores reales.

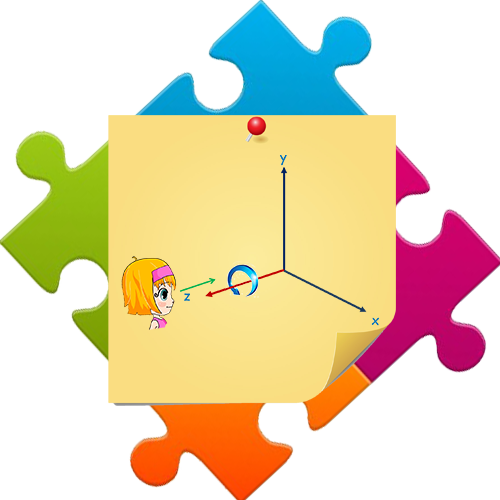
Rotación

Para generar una transformación de rotación para un objeto, se debe designar un eje de rotación  (con respecto del cual girará el objeto) y la cantidad de rotación angular. Una rotación tridimensional se puede especificar alrededor de cualquier línea en el espacio.

Las direcciones de rotación positivas con respecto de los ejes de las coordenadas son en sentido inverso al de las manecillas del reloj, cuando miramos hacia el origen de una posición de coordenadas positiva en cada eje.

Rotación de un objeto con respecto del eje de la z.

El parámetro θ especifica el ángulo de rotación. En la forma homogénea de las coordenadas, las ecuaciones de la rotación del eje de las z tridimensional se expresan como:

Rotación de un objeto con respecto del eje x

La representación matricial para la rotación del eje x es:

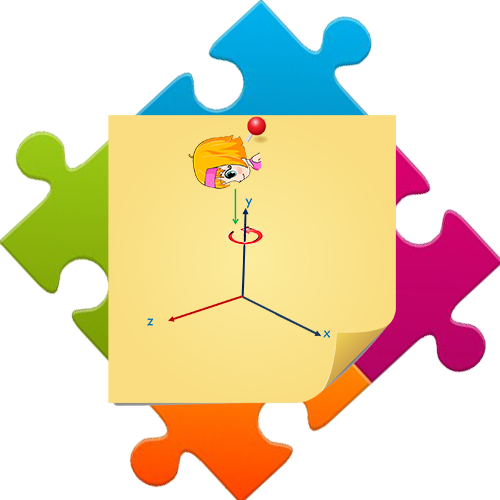
Rotación de un objeto con respecto del eje y

La forma matricial para representar la rotación del eje y es:

Escalación

La expresión matricial para la transformación de escalación de una posición P=(x,y,z)  con respecto del origen d las coordenadas se puede escribir como:

Donde  los parámetros de escalación s_x, s_y, s_z se asignan cualesquiera valores positivos.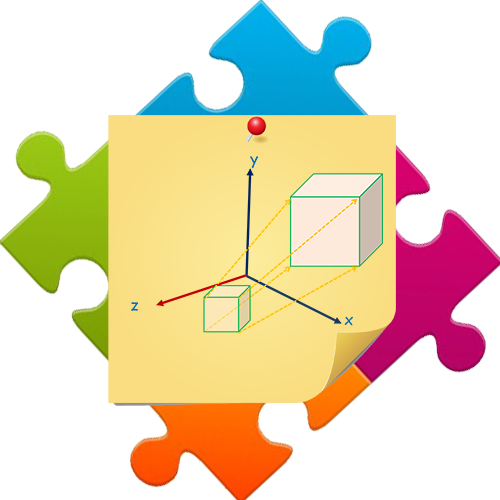