2.4.1 Propiedades de los Círculos
|
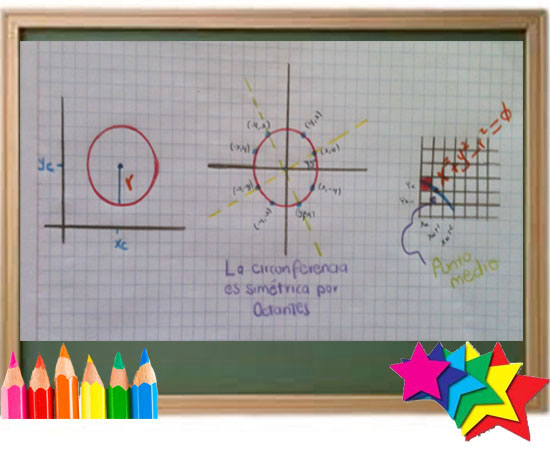
Una circunferencia se define como un conjunto de puntos que se encuentran, en su totalidad, a una distancia determinada r de una posición central (xc , yc). Esta relación de distancia se expresa por medio del teorema de Pitágoras en coordenadas cartesianas como (x - xc)2 + (y - yc)2 = r2 La forma de la circunferencia es similar en cada cuadrante. Se puede generar la sección circular del segundo cuadrante del plano de xy al notar que las dos secciones circulares son simétricas con respecto del eje de las y. Y las secciones circulares del tercero y el cuarto cuadrantes se pueden obtener a partir de las secciones del primero y el segundo cuadrantes al considerar la simetría en relación con el eje de las x. También se puede decir que hay simetría entre octantes. Las secciones circulares en octantes adyacentes dentro de un cuadrante son simétricas con respecto de la línea a 45° que divide los dos octantes. Al aprovechar la simetría de la circunferencia de esta manera, se podrá generar todas las posiciones de pixel alrededor de una circunferencia, calculando sólo puntos dentro del sector de x = 0 a x = y.
|