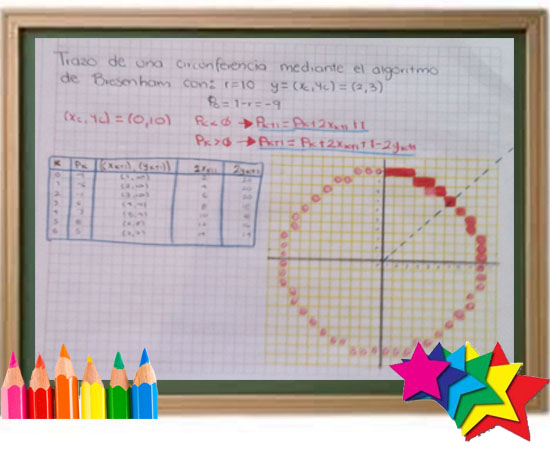
2.4.3 Algoritmo de Punto Medio - Bresenham

Al igual que en el algoritmo de la línea de rastreo, en el algoritmo de punto medio se efectúa un muestreo en intervalos unitarios y se determina la posición del pixel más cercano a la trayectoria específica de la circunferencia en cada paso. Para un radio r determinado y una posición central en la pantalla (x_c ,y_c), se puede establecer primero el algoritmo para calcular las posiciones de pixel alrededor de una trayectoria circular centrada en el origen de coordenadas (0,0). Así, cada posición calculada (x , y) se mueve a su posición propia en la pantalla al sumar x_c,a x y y_c a y.  A lo largo de la sección circular de x =0 a x = y en el primer cuadrante, la pendiente de la curva varía entre 0  y -1. Por tanto, se puede tomar pasos unitarios en la dirección positiva de x en este octante y utilizar un parámetro de decisión para determinar cuál de las dos posiciones posibles de y está más próxima a la trayectoria de la circunferencia en cada paso. Las posiciones de los otros siete octantes se obtienen entonces por simetría.

Para aplicar el método punto medio, se debe definir una función de circunferencia como:

f _{circunferencia} (x , y)= x² + y² - r²

f _{circunferencia} (x , y)= 0. Si el punto estpa en el interior de la circunferencia, la función de la circunferencia es negativa; y si está en su exterior, es positiva

Al igual que en el algoritmo para el trazo de líneas de Bresenham, el método del punto medio calcula las posiciones de pixel a lo largo de una circunferencia utilizando adiciones y sustracciones  de enteros, si se supone que los parámetros de la circunferencia se especifican en coordenadas enteras de pantalla. Se pueden resumir los pasos del algoritmo de la circunferencia de punto medio como sigue:

1.  Se capturan el radio r y el centro de la circunferencia (x_c , y_c) y se obtiene el primer punto de una circunferencia centrada en el origen como (x₀ , y₀) = (0 ,r).

2.  Se calcula el valor inicial del parámetro de decisión como p₀ = 5/4 - r.

3.  En cada x_k posición, al iniciar en k = 0, se realiza la prueba siguiente. Si p_k < 0, el siguiente punto a lo largo de la circunferencia centrada en (0 , 0) es (x_{k+1 ,} y_k) y p_k+1 = p_k +2x_k+1 +1. De otro modo, el siguiente punto a lo largo de la circunferencia es (x_k + 1, y_k -1) y p_k+1 = p_k + 2x_k+1 + 1 -2y_k+1 donde 2x_k+1 = 2x_k + 2 y 2y_k+1 = 2y_k -2.

4.  Se determinan puntos de simetría en los otros siete octantes.

5.  Se mueve cada posición de pixel calculada (x , y) a la trayectoria circular centrada en (x_c , y_c)setrazan los valores de las coordenadas: x = x + x_c     y= y + y_c .

6.  Se repiten los pasos 3 a 5 hasta que x ≥ y. 

Volver arriba