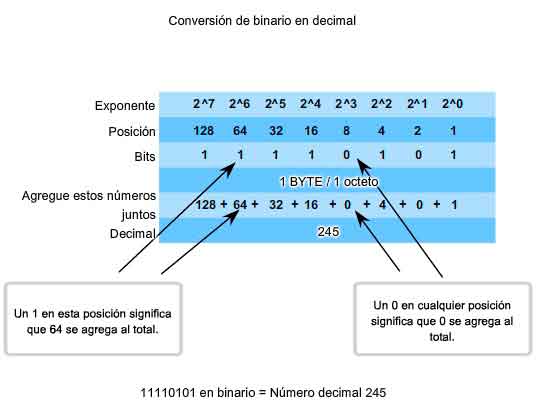
1.4.1 Binario-Decimal, Decimal-Binario

• BINARIO-DECIMAL:

Aprender a convertir el sistema binario a decimal requiere el conocimiento de los fundamentos matemáticos de un sistema de numeración denominado notación de posición. Notación de posición significa que un dígito representa diferentes valores según la posición que ocupa. Más específicamente, el valor que un dígito representa es el valor multiplicado por la potencia de la base o raíz representado por la posición que el dígito ocupa. Algunos ejemplo ayudarán a aclarar cómo funciona este sistema.

Para el número decimal 245, el valor que el 2 representa es 2*10^2 (2 multiplicado por 10 elevado a la segunda potencia). El 2 se encuentra en lo que comúnmente llamamos la posición "100". La notación de posición se refiere a esta posición como posición base^2 porque la base o raíz es 10 y la potencia es 2. Usando la notación de posición en el sistema de numeración con base 10, 245 representa:

245 = (2 * 10^2) + (4 * 10^1) + (5 * 10^0)

o

245 = (2 * 100) + (4 * 10) + (5 * 1)

Sistema de numeración binaria

En el sistema de numeración binaria la raíz es 2. Por lo tanto, cada posición representa potencias incrementadas de 2. En números binarios de 8 bits, las posiciones representan estas cantidades:

2^7 2^6 2^5 2^4 2^32^2 2^1 2^0

128 64 32 16 8 4 2 1

El sistema de numeración de base 2 tiene solamente dos dígitos: 0 y 1.

Cuando se interpreta un byte como un número decimal, se obtiene la cantidad que esa posición representa si el dígito es 1 y no se obtiene la cantidad si el dígito es 0, como se muestra en la figura.

1 1 1 1 1 1 1 1

128 64 32 16 8 4 2 1

Un 1 en cada posición significa que sumamos el valor para esa posición al total. Ésta es la suma cuando hay un 1 en cada posición de un octeto. El total es 255.

128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255

Un 0 en cada posición indica que no se suma el valor para esa posición al total. Un 0 en cada posición produce un total de 0.

0 0 0 0 0 0 0 0

128 64 32 16 8 4 2 1
0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0

Note en la figura que una combinación diferente de unos y ceros producirá un valor decimal diferente.

• DECIMAL-BINARIO:

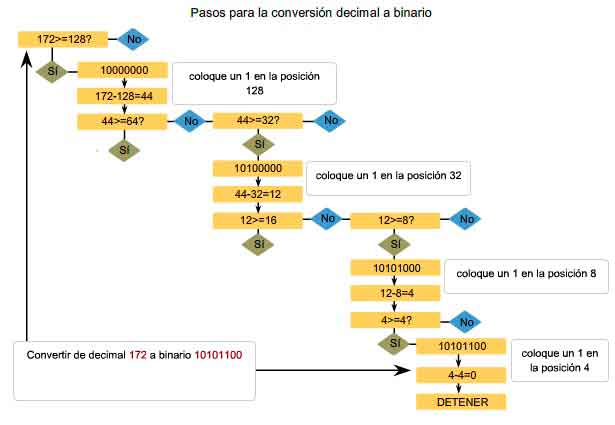
Examinaremos sólo el proceso de conversión binaria de 8 bits a valores decimales de 0 a 255 porque nuestra representación de direcciones está limitada a valores decimales para un solo octeto.

Para comenzar el proceso de conversión, empezaremos determinando si el número decimal es igual a o mayor que nuestro valor decimal más grande representado por el bit más significativo. En la posición más alta, se determina si el valor es igual o mayor que 128. Si el valor es menor que 128, se coloca un 0 en la posición de 128 bits y se mueve a la posición de 64 bits.

Si el valor en la posición de 128 bits es mayor o igual que 128, se coloca un 1 en la posición 128 y se resta 128 del número que se está convirtiendo. Luego se comparan los valores restantes de esta operación con el siguiente valor más pequeño, 64. Se continúa con este proceso para todas las posiciones de bits restantes.

Vea la figura para obtener un ejemplo de estos pasos. Se convierte 172 en 10101100.