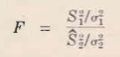7.4-En Relación a Varianza
|
ENSAYOS ESPECIALES DE SIGNIFICACION PARA PEQUEÑAS MUESTRAS En el caso de pequeñas muestras (n < 30) podemos formular ensayos de hipótesis y significación utilizando otras distribuciones además de la normal. como la t de Student, chi-cuadrado, F, etc. Estas distribuciones incluyen la teoría de muestreo exacto y lógicamente son válidas aún cuando las muestras son grandes, en cuyo caso se reducen a las dadas anteriormente. Para ensayar la hipótesis H0 de que una población normal tiene varianza σ2 consideramos la variable aleatoria:
Figura 7.4.1 Distribución Chi Cuadrado (n-1) º de libertad.
Relaciones de Varianzas
En algunos problemas deseamos decidir si dos muestras de tamaños m y n respectivamente, cuyas varianzas medidas son s21 y s22, provienen o no de la misma población normal. En este caso utilizamos el estadístico...
Figura 7.4.1 Relaciones de Varianzas. Donde σ21 y σ22 son
las varianzas de las dos poblaciones
normales de donde se extraen las muestras.
Si H0 denota la hipótesis nula
de que no hay diferencia entre las
varianzas poblacionales, es decir σ21
= σ22. (Murray R., 1976)
ASPECTOS A CONSIDERAR DE LA UNIDAD 7 Da Click En La Imagen Para Ver El Video
(Monardes, 2012)
|