1.2-Formas de Presentación de Información Estadística

La presentación de datos es uno de los aspectos de mas uso en la estadística descriptiva.

DATOS QUE MANEJA LA ESTADISTICA

• DATOS EXPERIMENTALES: Representa conteos o revisiones (se representan mediante números).

• DATOS CRITICOS: Se obtienen de acuerdo a un criterio o característica (color, brillo, acabado, textura).

• POBLACIÓN: Conjunto de datos que conforman los elementos que se desean estudiar.

• MUESTRA: Es una colección de algunos elementos pero no de todos. 

• MUESTRA REPRESENTATIVA: Es una muestra que contiene las características más relevantes de la población en la misma proporción que está incluida en esta.

• ORDENACIÓN DE DATOS: Es una de las formas más sencillas de presentar los datos puede ser de forma ascendente o descendente. La ordenación o arreglo de datos ofrece varias ventajas con respecto a los datos. Por Ejemplo:

1. Podemos nombrar rápidamente dos valores (mayor y menor de los datos).
2. Podemos fácilmente dividir los datos en secciones.
3. Podemos ver si alguno de los valores aparecen más de una vez en el ordenamiento.
4. Podemos observar la distancia entre los valores sucesivos de los datos.

     A pesar de las ventajas, en ocasiones un ordenamiento de datos no resulta del todo útil, esto es debido a que se crea una gran lista con todos los valores, lo que lo hace incomodo al momento de visualizar los datos, por ello se hace necesario comprimir la información, sin soslayar que uno debe ser capaz de utilizarla para su interpretación y toma de decisiones posteriores.

PRESENTACIÓN DE LA INFORMACIÓN

1-Presentación escrita: Se usa con pocos valores,  se hace de manera escrita,  resaltando la importancia de las informaciones principales.

2-Presentación tabular: representado mediante un conjunto de filas y de columnas, constituye la forma más exacta de presentar las informaciones. Sus partes son:

• Titulo: Describe todo él contenido.
• Encabezados: Subtítulos de cada columna.
• Columna matriz: Es la columna principal.
• Cuerpo: Son todas las informaciones numéricas que aparecen en la tabla.
• Fuente: Procedencia de los Datos.
• Notas al pie: Aclaraciones sobre algunos aspectos que no han sido explicados.

3-Presentación gráfica: Es  una expresión artística usada para representar un conjunto de datos. Por ejemplo:

• Histograma: Un histograma consiste en una serie de rectángulos cuyo ancho es proporcional al alcance de los datos que se encuentran sobre una clase y cuya altura es proporcional al número de elementos que cae dentro de la clase, dichos rectángulos están unidos uno de otro (Variables continuas). El histograma de frecuencia relativa, como su nombre lo indica, utiliza la frecuencia relativa en cada una de sus clases.
• Polígono de frecuencias: Es el polígono trazado uniendo los puntos localizados con las frecuencias y los puntos medios de las clases correspondientes, (se puede construir también el polígono de frecuencias relativo).

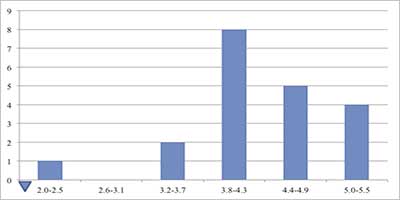
Figura 1.2.1 Polígono de Frecuencias

                2.6 - 2.5

P.M=  ____________ = 0.05

                    2

PUNTO MEDIO DE CLASE=     Mayor Valor - Menor Valor

                                                  _______________________ = .25

                                                                         2

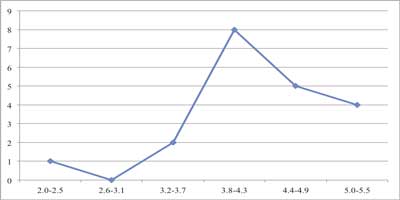
Figura 1.2.2 Histograma

Los histogramas y polígonos de frecuencia tienen ciertas ventajas; las ventajas de los histogramas son:

1. 1. Los rectángulos muestran cada clase de la distribución por separado.
   2. El área de cada rectángulo en relación con el resto muestra la proporción del número total de observaciones que se encuentran en cada clase

Las ventajas de los polígonos de frecuencia son:

1. 1. El polígono de frecuencia es más sencillo que su correspondiente histograma.
   2. Traza con más claridad el perfil del patrón de datos.
   3. El polígono se vuelve cada vez más liso y parecido a una curva conforme aumenta el número de clases y el número de observación.

• Gráfica de barras: Son barras separadas una de la otra (variables discretas); las barras deben ser de igual ancho y separadas a igual distancia. Pueden disponerse en forma vertical y horizontal.
• Gráfica lineal: Se usan para representar series de tiempo o cronológicas.
• Gráfica circular: Representa las partes en que se divide una cantidad total.
• La ojiva: Es una distribución de frecuencias acumuladas la cual nos permite ver cuantas observaciones están por encima de ciertos valores; a la gráfica de distribución de frecuencias acumuladas se le conoce como OJIVA.

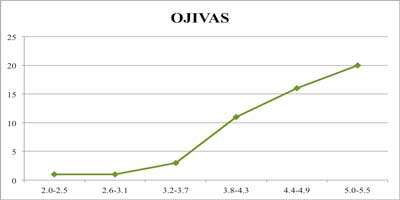
Figura 1.2.3 Histograma

DISTRIBUCIÓN DE FRECUENCIAS

Es una forma en que podemos comprimir los datos mediante una tabla conocida como "tabla de frecuencias", en ella, se organizan los datos en clases, una clase es una agrupación de valores o elementos con el cual vamos a comprimir a los datos en base a una frecuencia, que será el número de valores o  elementos que hay en cada clase, también existe la frecuencia relativa, que es la fracción o porcentaje del número total de cada frecuencia respecto al número total de la observación. Ejemplo de una tabla de Frecuencias:

TEMPERATURA Datos: 52, 80, 72, 52, 90, 80, 100, 59, 63, 99.

     El número de clases depende del número de datos y del alcance de los datos recolectados (alcance: Es la diferencia entre el valor mayor y el menor de los datos) cuantos más datos se tengan o más grande sea el alcance, más clases se necesitarán para dividir los datos. Desde luego si solamente tenemos diez datos no tendría sentido proponer diez clases. Como regla general los estadísticos utilizan rara vez menos de seis clases o más de 15 clases. Aunque la Regla de Sturges nos puede ayudar a determinar el número de estas.

REGLA DE STURGES

Número de clases= 1+3.3 log N

N= Número de datos

Número de clases= 1+3.3 log (20)= 5.9 ≈ 5 clases

Escala de               Alcance                     5.5-20

                     =  _____________      =  ________  = 0.58 ≈ .6

 La clase           Número de clases             6

(Levin I. & S. Rubin, 1996)

ARRIBA