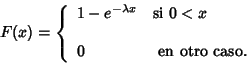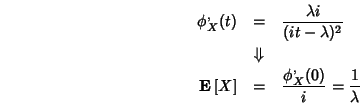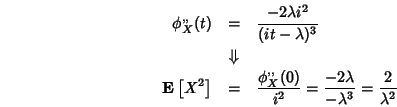|
DISTRIBUCIÓN EXPONENCIAL
La distribución exponencial es el equivalente continuo de la distribución geométrica discreta. Esta ley de distribución describe procesos en los que:
- Nos interesa saber el tiempo hasta que ocurre determinado evento, sabiendo que,
- El tiempo que pueda ocurrir desde cualquier instante dado t, hasta que ello ocurra en un instante tf, no depende del tiempo transcurrido anteriormente en el que no ha pasado nada.
Ejemplos de este tipo de distribuciones son:
- El tiempo que tarda una partícula radiactiva en desintegrarse. El conocimiento de la ley que sigue este evento se utiliza en Ciencia para, por ejemplo, la datación de fósiles o cualquier materia orgánica mediante la técnica del carbono 14, C14;
- El tiempo que puede transcurrir en un servicio de urgencias, para la llegada de un paciente;
- En un proceso de Poisson donde se repite sucesivamente un experimento a intervalos de tiempo iguales, el tiempo que transcurre entre la ocurrencia de dos sucesos consecutivos sigue un modelo probabilístico exponencial. Por ejemplo, el tiempo que transcurre entre que sufrimos dos veces una herida importante.
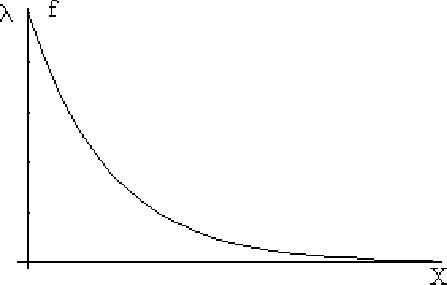
Concretando, si una v.a. continua X distribuida a lo largo de, es tal que su función de densidad es
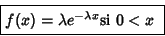
Figura 5.2.1 Función de Densidad
se dice que sigue una distribución exponencial de parámetro.
Figura 5.2.2 Función de densidad.
|
|
Un cálculo inmediato nos dice que si x>0,
luego la función de distribución es:
Imagen 5.2.3 Función De Distribución
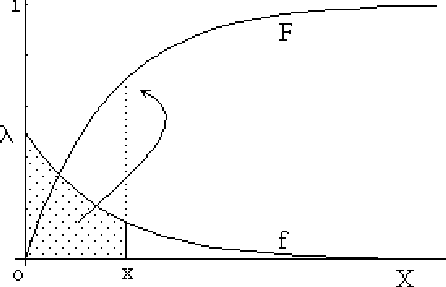
Figura 5.2.4 Función de distribución, F, calculada como el área que deja por debajo de sí la función de densidad.
|
|
Para calcular el valor esperado y la varianza de la distribución exponencial, obtenemos en primer lugar la función característica
para después, derivando por primera vez
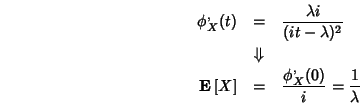
y derivando por segunda vez,
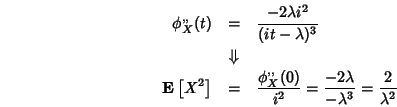
Entonces la varianza vale
Figura 5.2.5 Varianza
(P. Armitage, & G. Berry, 1992)
ARRIBA
|