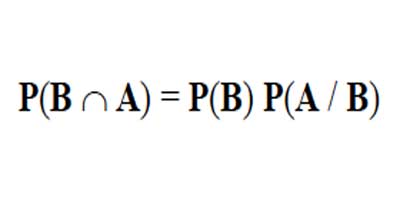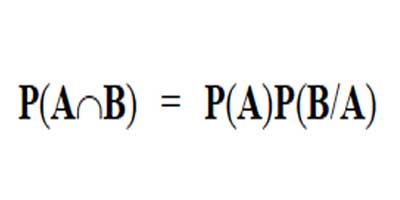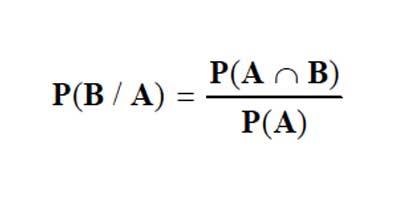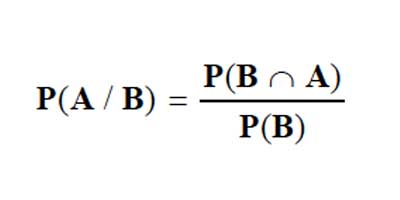2.3-Probabilidad Condicional
|
La probabilidad condicional se simboliza P(BnA), que se lee probabilidad de B, dado A, o la probabilidad de que ocurra B, condicionado a que haya ocurrido A. Se dice que dos o más eventos son independientes entre sí cuando la probabilidad de que ocurra uno no es influida por la ocurrencia de otro. Si A y B representan dos eventos y si la ocurrencia de A no afecta a la ocurrencia de B, y la ocurrencia de B no afecta a la ocurrencia de A, entonces se dice que A y B son Independientes. En este caso, la probabilidad de que ocurran A y B es igual al producto de sus respectivas probabilidades, y se expresa así:
En una caja hay 5 esferas blancas, 4 rojas y 3 negras. Se extrae una esfera, se observa su color y se regresa a la caja. Bajo estas condiciones, ¿Cuál es la probabilidad de que al extraer 3 esferas, éstas sean de color rojo?
Si dos eventos A y B no son independientes, es decir, si A y B son dependientes, la probabilidad compuesta de A y B no es igual al producto de sus probabilidades respectivas. Por lo cual, podemos decir, que para eventos dependientes:
Es decir:
ó
Figura 2.3.3 Probabilidad De Eventos Dependientes
En una caja hay 5 esferas blancas, 4 rojas y 3 negras. Si se extraen al azar 3 esferas en forma consecutiva, sin reemplazo, ¿ Cuál es la probabilidad de que las 3 sean de color rojo? Sea R1 el evento extraer una esfera roja.
De la expresión
Despejamos P(B/A) y se obtiene la probabilidad condicional de "B dado A".
En forma análoga, la probabilidad condicional de "A dado B", es :
(Obregón Sanin Ivón, 1975)
|
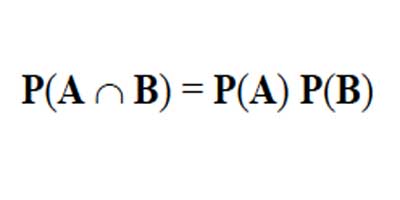Figura 2.3.1 Probabilidad Condicional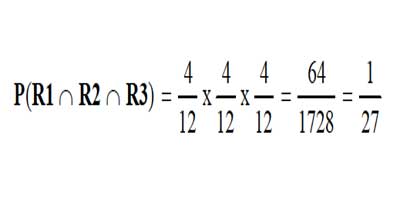
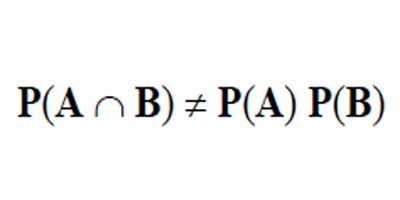Figura 2.3.3 Probabilidad De Eventos Dependientes
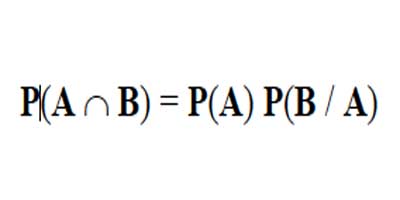Figura 2.3.4 Probabilidad De Eventos Dependientes
