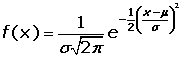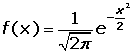5.1-Normal y Normal Estándar
|
Una variable aleatoria continua, X, sigue una distribución normal de media μ y desviación típica σ, y se designa porN(μ, σ), si se cumplen las siguientes condiciones: 1. La variable puede tomar cualquier valor: (-∞, +∞) 2. La función de densidad, es la expresión en términos de ecuación matemática de la curva de Gauss:
Figura 5.1.1 Función de Densidad Curva de la distribución normal
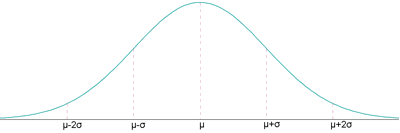
Figura 5.1.2 Curva de la distribución normal
* El campo de existencia es cualquier valor real, es decir, (-∞, +∞). * Es simétrica respecto a la media µ. * Tiene un máximo en la media µ. * Crece hasta la media µ y decrece a partir de ella. * En los puntos µ − σ y µ + σ presenta puntos de inflexión. * El eje de abscisas es una asíntota de la curva.
El área del recinto determinado por la función y el eje de abscisas es igual a la unidad. Al ser simétrica respecto al eje que pasa por x = µ, deja un área igual a 0.5 a la izquierda y otra igual a 0.5 a la derecha. La probabilidad equivale al área encerrada bajo la curva.
p(μ - σ < X ≤ μ + σ) = 0.6826 = 68.26 % p(μ - 2σ < X ≤ μ + 2σ) = 0.954 = 95.4 % p(μ - 3σ < X ≤ μ + 3σ) = 0.997 = 99.7 %
DISTRIBUCIÓN NORMAL ESTÁNDARLa distribución normal estándar, o tipificada o reducida, es aquella que tiene por media el valor cero, μ =0, y pordesviación típica la unidad, σ =1. Su función de densidad es:
Figura 5.1.3 Distribución Normal Estándar Su gráfica es:
Figura 5.1.4 Gráfica de la Distribución Normal Estándar
La probabilidad de la variable X dependerá del área del recinto sombreado en la figura. Y para calcularla utilizaremos una tabla. Tipificación de la variablePara poder utilizar la tabla tenemos que transformar la variable X que sigue una distribución N(μ, σ) en otra variable Z que siga una distribución N(0, 1).
Figura 5.1.5 Tipificación de la Variable (Cedeño, 2013) |