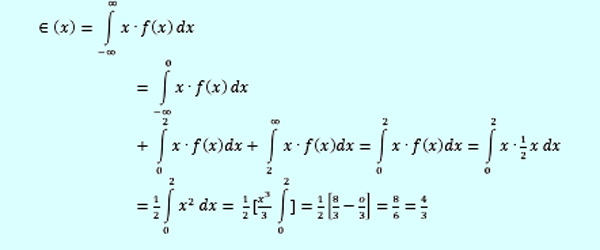3.3-Funciones de Distribución de Probabilidad y de Densidad.

DISTRIBUCIONES DE PROBABILIDAD Y DENSIDAD

• DISTRIBUCIÓN DE PROBABILIDAD DISCRETA: Sea X una variable aleatoria discreta y suponga que los valores posibles que puede tomar están dados por x1, x2, x3,…, xk ordenado en orden de 100 de magnitud supóngase también que los valores se asumen con probabilidades dadas por:

P(X=xk) = f (xk)

K= 1, 2, 3,…, ∞ 

Es conveniente introducir la función de probabilidad conocida también como la distribución de probabilidad definida como la siguiente forma:

P (X=x) = f(x)

En general f(x) es una función de probabilidad si se cumple con lo siguiente:

1)    F(x1)¸0

2)    ∑ f(Xi) = 1

FUNCIÓN DE DISTRIBUCIÓN ACUMULADA: La distribución acumulada posiblemente la función de distribución para una variable aleatoria X se define por:

P(X.x) = f (x)

Dónde:

X cualquier número real es decir: -∞ < x < ∞

La función de distribución acumulada puede obtenerse de la función de probabilidad notando que:

F(x) = P (X.x)= ∑ f (u)                                                  para -∞ < x < ∞

Si x únicamente toma un número finito de valores entonces la función de distribución está dada por la siguiente función:

              0                                      si            -∞ < x < x1

              f(x1)                                si             x1 . x < x2

F(x)=    f(x1) + f(x2)                    si             x2 . x < x3

              f (x1)+f(x2)+…+f (xn)   si             Xn  x < +∞

• DISTRIBUCIÓN DE PROBABILIDAD CONTINUA: Si X es una variable aleatoria continua la probabilidad de que X tome un valor determinado en cero. Por lo tanto no podemos definir una función de probabilidad en la misma forma que para una variable aleatoria discreta sin embargo para una variable continua notamos que la probabilidad de x se encuentre entre dos valores diferentes tienen significado.La probabilidad de x se encuentre entre dos valores diferentes tienen significado.Las ideas anteriores y las analógicas vistas anteriormente permiten postular la existencia de una función f(x) de manera que se tienen las siguientes definiciones. Para la variable aleatoria X definida en el conjunto de los números reales si:

∫_(-∞)^∞ 〖f(x)dx=1〗

P(a< x <b)= ∫_a^b f(x)dx

Como consecuencia de lo anterior se tiene la siguiente definición:

La distribución acumulada f(x) de una variable aleatoria continúa de X con una función de densidad  f(x) es:

F(x)= P(X.x) = ∫_(-∞)^x〖f(t)dt para-∞<x< ∞〗

También se puede escribir el siguiente resultado:

P(a< X <b)= f (b)- f(a)

Ejemplo:  Un empate de 5 automóviles extranjeros influye 2 que tienen unas ligeras manchas de pintura. Si una agencia recibe 3 de estos automóviles aleatoriamente indique los elementos del espacio muestral 5 utilizando las letras M y B para manchado y uno no manchado respectivamente. Para cada uno el valor x de la variable x que representa el número de x con manchas de pintura comprados por la agencia.

La función de densidad de una variable aleatoria f está dada por:

               ½ x         si      0< x <2

Hallar la probabilidad de dicha función.

P (0< x <2) = ∫_0^2〖1/2 x dx=1/2 ∫_0^2〖x dx〗=1/2[(xˆ2)/2]〗= ½ (4/2)=1

Si x tiene la densidad de probabilidad

       K e^(-3x) para x >0

F(x)= 0 cualquier otra parte

 Encuentre el valor k y la probabilidad P (0.5< x <y)

∫_(-∞)^∞ 〖f(x)dx=1〗

∫_(-∞)^∞ 〖f(x)dx=∫_(-∞)^0〖f(x)dx+ ∫_0^∞f(x)dx〗〗

= ∫_0^∞〖K e^(-3x)  dx=1〗

k∫_0^∞ 〖e^(-3x) dx= -k/3 ∫_0^∞〖(-3) e^(-3x) 〗  dx= -k/3[e^(-3x)]〗

-k/3 (-1)→  k/3=1

S= {BBB, BBM, BMM, MBM, MMB, BMB, MBB}

f (0) = P (M=0) = BBB= 1/7

f (1)=P (M=1)= BBB, BMM, MBM = 3/7

f (2)= P (M=2)= MMB, BMM, MBM= 3/7

∑= f (M)=1

Determine el valor de C de tal forma que la siguiente función sirva como una distribución de probabilidad de la variable aleatoria X.

F(x)= C (xˆ2+4) para x= 0, 1, 2, 3

f (0)+f (1)+f (2)+f (3)=1

f (0)=4

f (1)=5

f (2)=8

f (3)=13

 ∑f(x) =30

30C=1

C=1/30

DISTRIBUCIONES DE DENSIDAD

Para una variable aleatoria continua x que tiene una función de densidad f(x) la esperanza de x se define como:

∈(x)=∫(-∞)^∞ 〖x∙f(x)dx〗

La función de densidad de una variable aleatoria  x está dada por:

(1/2) x   si 0<x<2

f(x)={

0 de otra forma

Hallar el valor esperado de x

 Figura 3.3.1 Distribución de densidad

(Quevedo Urías, 2006)

ARRIBA