2.5-Eventos Independientes
|
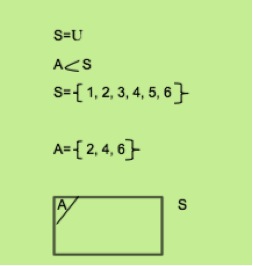
Es un subconjunto de un espacio mostrado, es el conjunto que contiene a todos los elementos, se puede considerar como el Conjunto Universo. Ejemplo: El experimento de lanzar un dado entonces un evento A puede ser el numero obtenible es divisible.
Figura 2.5.1 Evento
EVENTOS INDEPENDIENTES Dos eventos A y B son independientes si la ocurrencia de cualquiera de los dos no afecta la probabilidad de la ocurrencia DEFINICIÓN: Dos eventos A y B son independientes si y solo si la probabilidad de la intersección es igual a la probabilidad de A y B P (A\B) = P (A) * P (B) EJEMPLO 1: Se lanza una moneda 3 veces y se supone que los 8 resultados posibles son igualmente probables. {SSS, SSA, SAS, ASS, SAA, ASA, AAS, AAA} Si A es el evento de que un sol ocurra en cada uno de los primeros lanzamientos B es el evento de un águila ocurren en el tercer lanzamiento C es el evento que exactamente dos cruces ocurran en tres lanzamientos. Demuestre que: a) Los eventos A y B son independientes b) Los eventos B y C son independientes A= SSS, SSA B= SSA, SAA, ASA, AAA C= SAA, ASA, AAS, AAA 0.125=0.25*0.5 0.125=0.125 0.375=0.5*0.5 0.375=0.375 Encuentre las probabilidades de obtener a) Tres caras en 3 lanzamientos aleatorios de una moneda balanceada b) Se obtienen 4 seises y después otro número en 5 lanzamientos aleatorios de un dado balanceado
½*1/2*1/2*1/2= 1/8 P (A)= 1/8= 0.125 P (B)= 1/6 * 1/6 * 1/6 * 1/6= 0.00077*5/6=0.00064
EJEMPLO 2: Suponga que de una baraja de: 52 cartas ( 26 cartas rojas y 26 cartas negras ) Se sacan 2 cartas. ¿Cuál es la probabilidad de que ambas sean rojas y mayores que 3 pero menores que 8? P (A\B)= P (A) P (B|A)
Figura 2.5.2 Eventos Independientes
(E. Walpole, H. Myers, & L. Myers, 2012)
ASPECTOS A CONSIDERAR DE LA UNIDAD 2 Da Click En La Imagen Para Ver El Video (LuisRinconUNAM, 2013)
|