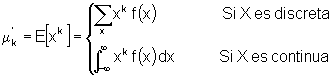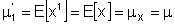3.4-Cálculo e Interpretación de Momentos
|
Los momentos de una variable aleatoria X son los valores esperados de ciertas funciones de X. Estos forman una colección de medidas descriptivas que pueden emplearse para caracterizar la distribución de probabilidad de X y especificaciones si todos los momentos de X son conocidos. MOMENTOS RESPECTO DEL ORIGEN Dada una variable aleatoria X con función de probabilidad o densidad f(x) podemos definir una función de X que sea igual a la variable elevada a un exponente entero no negativo.
Figura 3.4.1 Definición De Momento
K = 0 K = 1
Figura 3.4.2 Valor Esperado de z(x)
A este primer momento respecto al origen que es igual al valor esperado se le llama también media aritmética de la variable y se le denomina Mx, simplemente M. En la mayoría d ellos casos, la media M expresa la tendencia central de la variable o el orden de magnitud de sus valores. El resto de los momentos respecto al origen tiene escaso interés en la mayoría de los casos. (Quevedo Urías, 2006)
|