7.1-De Una o Dos Colas
|
Muy a menudo, en la práctica se tienen que tomar decisiones sobre poblaciones, partiendo de la información muestral de las mismas. Tales decisiones se llaman decisiones estadísticas. Por ejemplo, se puede querer decidir a partir de los datos del muestreo, si un suero nuevo es realmente efectivo para la cura de una enfermedad, si un sistema educacional es mejor que otro, si una moneda determinada está o no cargada, etc.
HIPOTESIS NULA
Para llegar a tomar decisiones, conviene hacer determinados supuestos o conjeturas acerca de las poblaciones que se estudian. Tales supuestos que pueden ser o no ciertos se llaman hipótesis estadísticas y en general, lo son sobre la distribución de probabilidad de las poblaciones. En muchos casos se formulan las hipótesis estadísticas con el solo propósito de rechazarlas o invalidarlas. Por ejemplo, si se quiere decidir si una moneda está cargada, se formula la hipótesisde que la moneda está bien, es decir, p = 0.5; donde p es la probabilidad de cara. Análogamente, si se quiere decidir sobre si un procedimiento es mejor que otro, se formula la hipótesis de que no hay diferencia entre ios procedimientos (es decir, cualquier diferencia observada se debe meramente a fluctuaciones en el muestreo de la misma población) Tales hipótesis se llaman también hipótests nulas y se denotan por Ho . Cualquier hipótesis que difiera de una hipótesis dada se llama hipótesis alternativa. Por ejemplo, si una hipótesis es p=0.5, hipótesis alternativas son p=0.7; p≠0.56 ó p>0.5. Unahipótesis alternativa de la hipótesis nula se denota por H1 .
ENSAYOS DE HIPÓTESIS Y SIGNIFICACIÓN
Si en el supuesto de que una hipótesis determinada es cierta, se encuentra que los resultados observados en una muestra aleatoria difieren marcadamente de aquellos que cabía esperar con la hipótesis y con la variación propia del muestreo, se diría que las diferencias observadas son significativas y se estaría en condiciones de rechazar la hipótesis (o al menos no estaría de acuerdo con la evidencia obtenida). Por ejemplo, si en 20 lanzamientos de una moneda se obtienen 16 caras, se estaría inclinado a rechazar la hipótesis de que la moneda está bien, aunque sería posible que fuese un rechazamiento erróneo. Los procedimientos que facilitan el decidir si una hipótesis se acepta o se rechaza o el determinar si las muestras observadas difieren significativamente de los resultados esperados se llaman ensayos o pruebas de hipótesis, ensayos de significación o reglas de decisión.
ERRORES TIPO I Y TIPO II Si se rechaza una hipótesis cuando debería ser aceptada, se dice que se comete un error del Tipo i. Si por el contrario, se acepta una hipótesis que debería ser rechazada, se dice que se comete un error del Tipo II. En cualquiera de los dos casos se comete un error al tomar una decisión equivocada. Para que cualquier ensayo de hipótesis o reglas de decisión sea bueno, debe diseñarse de forma que minimice los errores de decisión. Esto no es tan sencillo como pueda parecer puesto que para un tamaño de muestra dado, un intento de disminuir un tipo de error, va generalmente acompañádo por un incremento en el otro tipo de error. En la práctica, un tipo de error puede tener más importancia que el otro, y así se tiende a conseguir poner una limitación al error de mayor importancia. La única forma de reducir al tiempo ambos tipos de errores es incrementar el tamaño de la muestra, lo cual puede o no ser posible.
NIVEL DE SIGNIFICACION La probabilidad máxima con la que en el ensayo de una hipótesis se puede cometer un error del Tipo I se llama nivel de significación del ensayo. Esta probabilidad se denota frecuentemente por α; generalmente se fija antes de la extracción de las muestras, de modo que los resultados obtenidos no influyen en la elección. En la práctica se acostumbra a utilizar niveles de significación del 0.05 ó 0.01, aunque igualmente pueden emplearse otros valores. Si, por ejemplo se elige un nivel de significación del 0.05 ó 5% al diseñar un ensayo de hipótesis, entonces hay aproximadamente 5 ocasiones en 100 en que se rechazaría la hipótesis cuando debería ser aceptada, es decir, se está con un 95% de confianza de que se toma la decisión adecuada. En tal caso se dice que la hipótesis ha sido rechazada al nivel de significación del 0.05,lo que significa que se puede cometer error con una probabilidad de 0.05.
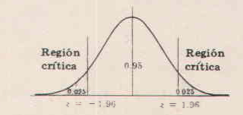
ENSAYOS REFERENTES A LA DISTRIBUCION NORMAL Para aclarar las ideas anteriores, supóngase que con una hipótesis dada, la distribución muestral de un estadístico S es una distribución normal con media μs y desviación típica σs. Entonces la distribución de la variable tipificada dada por Z = (S- μs )/ σs, es una normal tipificada (media 0, varianza 1) . Figura 7.1.1 Distribución Normal Como se indica en la figura, se puede estar con el 95% de confianza de que, si la hipótesis es cierta, el valor de z obtenido de una muestra real para el estadístico S se encontrará entre -1.96 y 1.96 (puesto que el área bajo la curva normal entre estos valores es 0.95). Sin embargo, si al elegir una muestra aleatoria se encuentra que z para ese estadístico se halla fuera del recorrido -1.96 a 1.96, lo que quiere decir que es un suceso con probabilidad de solamente 0.05 (área sombreada de la figura) si la hipótesis fuese verdadera. Entonces puede decirse que esta z difiere significativamente de la que cabía esperar bajo esta hipótesis y se estaría inclinado a rechazar la hipótesis. El área total sombreada 0.05 es el nivel de significación del ensayo. Representa la probabilidad de cometer error al rechazar la hipótesis, es decir, la probabilidad de cometer error del Tipo I. Así pues, se dice que la hipótesis se rechaza a nivel de significación del 0.05 o que la z obtenida del estadístico muestral dado es significativa al nivel de significación del 0.05. El conjunto de las z que se encuentran fuera del rango -1.96 a 1.96 constituyen lo que se llama región crítica o región de rechace de la hipótesis o región de significación. El conjunto de las z que se encuentran dentro del recorrido -1.96 a 1.96 podía entonces llamarse región de aceptación de h hipótesis o región de no significación. De acuerdo con lo dicho hasta ahora, se puede formular la siguiente regla de decisión o ensayo de hipótesis o significación:
Debe ponerse de manifiesto que pueden igualmente emplearse otros niveles de significación. Por ejemplo, si se utilizase el nivel de 0.01 se sustituría 1.96 en todo lo visto anteriormente por 2.58.
ENSAYOS DE UNA Y DOS COLAS En el ensayo anterior se mostraban los valores extremos del estadístico S o su correspondiente z a ambos lados de la media, es decir, en las dos "colas" de la distribución. Por esta razón, tales ensayos se llaman ensayos de dos colas , ensayos bilaterales o prueba de hipótesis de dos colas. Sin embargo, con frecuencia se puede estar solamente interesado en los valores extremos a un solo lado de Ia media, es decir, en una "cola" de la distribución, como por ejemplo, cuando se está ensayando la hipótesis de que un proceso es mejor que otro (que es diferente a ensayar si un proceso es mejor o peor que otro). Tales ensayos se llaman ensayos de una cola o ensayos unilaterales. En tales casos, Ia región crítica es una región a un lado de la distribución, con área igual al nivel de significación. La siguiente tabla da los valores críticos de z para ensayos de una y dos colas a distintos niveles de significación, será́ de utilidad para propósitos de referencia. Valores críticos de z para otros niveles de significación, se pueden encontrar utilizando la tabla que da las áreas bajo la curva normal.
(Murray R., 1976) |