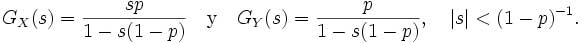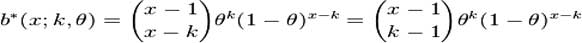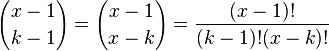4.1-Binomial, Multinomial, Geométrica y Binomial Negativa
|
VARIABLE ALEATORIA DISCRETA: Es una variable que toma un numero finito n un infinito contable de valores, es decir números enteros positivos incluyendo el 0. DISTRIBUCIÓN DE PROBABILIDAD DISCRETA: Sea X una variable aleatoria discreta y suponga que los valores posibles que puede tomar están dados por x1, x2, x3,…, xk ordenado en orden de 100 de magnitud supóngase también que los valores se asumen con probabilidades dadas por: P(X=xk) = f (xk) K= 1, 2, 3,…, ∞ Es conveniente introducir la función de probabilidad conocida también como la distribución de probabilidad definida como la siguiente forma: P (X=x) = f(x) En general f(x) es una función de probabilidad si se cumple con lo siguiente: 1) F(x1)¸0 2) ∑ f(Xi) = 1 Una gráfica de f(x) se llama grafica de probabilidad. Hallar la función de probabilidad correspondiente a la variable aleatoria x del ejemplo anterior. X= que salga sol f (0) = P (x=0)= ¼ f (0) = P (x=1)= 1/2 f (0) = P (x=2)= ¼
DISTRIBUCION BINOMIAL (de Bernoulli) Un experimento de Bernoulli puede resultar en un éxito con una probabilidad (p) y un fracaso con una probabilidad. q=1-ρ Entonces la distribución de probabilidad de la variable aleatoria binomial x para el número de éxitos en n experimentos es: b(x;n,ρ)=(nx)ρxqn-x NC La media y la varianza de la distribución binominal están dadas por: M= nρ √2=n ρ q
Con frecuencia el interés se centra en problemas donde es necesario encontrar: ρ(x<r) ρ(a ≤ x ≤ b) Para esto se dispone de las sumas binomiales... B(r;n,ρ)= ∑ rx=0 b(x;n,φ) Ejemplo: De acuerdo con un estudio público por un grupo de sociólogos de la Universidad Nacional Autónoma de México aproximadamente el % 60 de los adictos al Valium en el estado de México lo tomaron por primera vez debido a problemas psicológicos; encuentre la probabilidad de que los siguientes 8 adictos entrevistados: a) Exactamente 3 hallan comenzado a usarlo por problemas psicológicos b) Al menos 5 de ellos comenzaron a tomarlo por problemas que no fueron psicológicos n=8 x=3 Ƥ=0.60 q=0.40 b (3;8,0.6)=8C3(0.6)3(0.4)8-3 b (3;8,0.6)=0.123 p x >5=1- Ƥ(x<5) 1-(8/0)C 1-C0(0.40)0*ρ8+8C1(0.4)1*(0.6)6+8C3(0.4)3*(0.6)5+8C4(04)4*(0.6)4=0.167+0.0895+0.2090+0.2786+0.2322=0.82631-0.8263=0.1737
nCxφ^x q^(n-x) p(x=3)=∑_(i=0)^3 b (x;8,0.6)-∑_(i=0)^2 b (x;8,0.6) r=3 r=2 0.1737 – 0.0498 P(x=3) = 0.1239 DISTRIBUCION MULTINOMIAL En teoría de probabilidad, la distribución multinomial es una generalización de la Distribución Binomial. En una distribución multinomial, el análogo a la distribución de Bernoulli es la distribución categórica, donde cada suceso concluye en únicamente un resultado de un número finito K de los posibles, con probabilidades tal que... (Pi≥0 para i entre 1 y K y ∑k i=1 Pi=1); y con n sucesos independientes. Entonces
sea la variable aleatoria, que indica el número de
veces que se ha dado el resultado i sobre los n
sucesos. El vector x=(x1,...,xk) sigue una
distribución multinomial con parámetros n y p, donde
p=(p1,..., pk). La Función de probabilidad de la distribución multinomial es como sigue: f(x1, ..., xk; n, p1, pk)= Pr(x1=x1 y ... y Xk= xk) [ (n!)/(x1!...xk!) ] * (P1 x1... Pk xk ) cuando ∑k i=1 xi=n = 0 en otras casos Para enteros no negativos x1, ..., xk. PROPIEDADES
Una definición fácil de entender es la relación entre el premio obtenido y la probabilidad de acertar en para una variable aleatoria discreta y f(x) es el valor esperado de su distribución de probabilidad en x el valor esperado de x es: ϵ(x)=∑_(i=1)^n 〖xi∙f(xi) 〗
ALGUNOS TEOOREMAS SOBRE ESPERANZA MATEMATICA
∈(cx)=c∈(x)
∈(x+y)=∈(x)+∈(y)
∈(xy)=∈(x)∈(y) VARIANZA: una cantidad de gran importancia en probabilidad y estadística y se define como el valor esperado de: DESVIACION ESTANDAR: se define como la raíz cuadrada de la varianza del valor esperado. √R=√(var(x) )=√(∈(x-M)^2 ) Si x es una variable aleatoria discreta con función de probabilidad f(x) entonces la varianza es: √=∈[(x-M)^2 ]=∑_(i=1)^n〖(xi-M)^2∙f(xi) 〗
ALGUNOS TEOREMAS SOBRE VARIANZA
var(x+y)=var (x)+var (y) √(x+y)〗^2=〖√x〗^2+ 〖√y〗^2 var (x+y)=var(x)-var (y) 〖√(x+y)〗 ^2=〖√x〗^2- 〖√y〗^2
DISTRIBUCION GEOMÉTRICA En teoría de probabilidad y estadística, la distribución geométrica es cualquiera de las dos distribuciones de probabilidad discretas siguientes:
Sus propiedades: Si la probabilidad de éxito en cada ensayo es p, entonces la probabilidad de que x ensayos sean necesarios para obtener un éxito es P(X=X)=(1-p)x-1p para x = 1, 2, 3,.... Equivalentemente, la probabilidad de que haya x fallos antes del primer éxito es P(X=X)=(1-p)xp para x = 0, 1, 2, 3,....
En ambos casos, la secuencia de probabilidades es una progresión geométrica. El valor esperado de una variable aleatoria X distribuida geométricamente es: E(X) =1/p y dado que Y=X-1 E(Y) =(1/p)/p en ambos casos. la varianza es var(Y) = var(X) = (1/p)/p2 Las funciones generatrices de probabilidad de X y la de Y son, respectivamente.
Figura 4.1.1 Funciones Generatrices de Probabilidad
Como su análoga continua, la distribución exponencial, la distribución geométrica carece de memoria. Esto significa que si intentamos repetir el experimento hasta el primer éxito, entonces, dado que el primer éxito todavía no ha ocurrido, la distribución de probabilidad condicional del número de ensayos adicionales no depende de cuantos fallos se hayan observado. El dado o la moneda que uno lanza no tiene "memoria" de estos fallos. La distribución geométrica es de hecho la única distribución discreta sin memoria. La distribución geométrica del número y de fallos antes del primer éxito es infinitamente divisible, esto es, para cualquier entero positivo n, existen variables aleatorias independientes Y 1,..., Yn distribuidas idénticamente la suma de las cuales tiene la misma distribución que tiene Y. Estas no serán geométricamente distribuidas a menos que n = 1. DISTRIBUCION BINOMIAL NEGATIVA En estadística la distribución binomial negativa es una distribución de probabilidad discreta que incluye a la distribución de Pascal. El número de experimentos de Bernoulli de parámetro θ independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros k y θ. La distribución geométrica es el caso concreto de la binomial negativa cuando k = 1. PROPIEDADES Su función de Probabilidad es
Figura 4.1.2 Fórmula Binomial para enteros x mayores o iguales que k, donde
Figura 4.1.3 Fórmula Binomial Enteros mayores o iguales que k Su media es: μ= k(1-θ)/θ Si se piensa en el número de fracasos únicamente y μ= k/θ Si se cuentan también los k-1 éxitos su varianza es σ2=(k(1-θ))/θ2 en ambos casos. Ejemplo: Si la probabilidad de que un niño expuesto a una enfermedad contagiosa la contraiga es 0,40, ¿Cuál es la probabilidad de que el décimo niño expuesto a la enfermedad sea el tercero en contraerla? En este caso, X es el número de niños expuestos la enfermedad y x=10, k=1, θ=0.40 La solución es: b*(10;1,0.4)= (103--11)0.43(1-0.4)10-3=(92)0.43(0.6)7=0.0645 En un proceso de manufactura se sabe que un promedio de 1 en cada 10 productos es defectuoso, ¿Cuál es la probabilidad que el quinto (5) artículo examinado sea el primero (1) en estar defectuoso?. La solución es: X= artículos defectuosos P= 1/10 = 0,1 q= 1- 0,1 = 0,9 x= 5 ensayos K= 1 b*(5;1,0.1)=(5-1\1-1)(0.1)^1*(0.9)^5-1= b*(5;1,0.1)= 6.6% de probabilidad que el quinto elemento extraído sea el primero en estar defectuoso.
(Ibarra Mendívil, 2008)
|