7.3-Relacionadas con Proporciones
|
Pruebas de Hipótesis de Significación para grandes Muestras
Para muestras grandes, las distribuciones muéstrales de muchos estadísticos son distribuciones normales(o al menos casi normales) con media μs y desviación típica σs.
Aquí S = P, la proporción de "éxitos" en una muestra; μs=μp=p, donde p es la proporción de éxitos en la población y n es el tamaño de la muestra, σs=σp=√((pq)/n), donde q= 1-p .
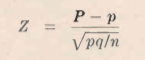
Figura 7.2.1 Variable tipificada.
Diferencias de Proporciones
Sean P1 y P2 las proporciones muestrales de dos grandes muestras de tamaños n1 y n2 extraídas de poblaciones respectivas que tienen proporciones p1 y p2. Considérese la hipótesis nula de que no hay diferencia entre los parámetros poblacionales, es decir, p1 = p2, y así las muestras son realmente extraídas de la misma población. Haciendo p, p1= p2= p.
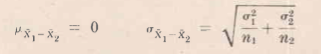
Figura 7.2.1 Distribución Normal con Media y Desviación Típica.
|
|