|
La distribución Uniforme es el modelo (absolutamente) continuo más simple. Corresponde al caso de una variable aleatoria que sólo puede tomar valores comprendidos entre dos extremos a y b, de manera que todos los intervalos de una misma longitud (dentro de (a, b)) tienen la misma probabilidad. También puede expresarse como el modelo probabilístico correspondiente a tomar un número al azar dentro de un intervalo (a, b).
De la anterior definición se desprende que la función de densidad debe tomar el mismo valor para todos los puntos dentro del intervalo (a, b) (y cero fuera del intervalo). Es decir,
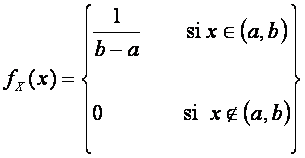 . .
Figura 5.3.1 Función de Densidad de la Distribución Uniforme
Gráficamente:
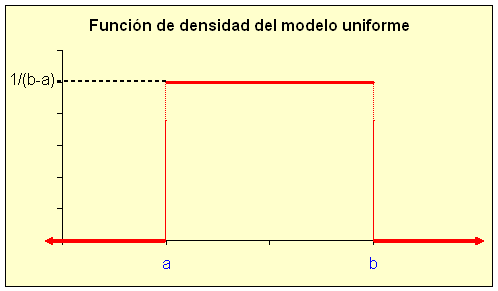
Figura 5.3.2 Función De Densidad del Modelo Uniforme
La función de distribución se obtiene integrando la función de densidad y viene dada por:
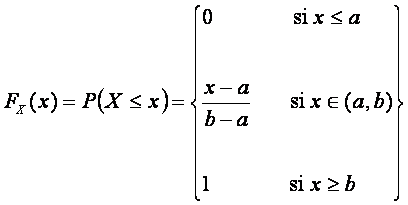
Figura 5.3.3 Función De Distribución
Gráficamente:
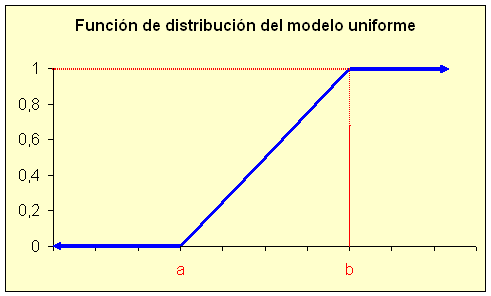
Figura 5.3.4 Función De Distribución Del Modelo Uniforme
Propiedades del modelo Uniforme
-
Su esperanza vale (b + a)/2
-
Su varianza es (b − a)2/12
(P. Armitage, & G. Berry, 1992)
ASPECTOS A CONSIDERAR DE LA UNIDAD 5
Da Click En La Imagen Para Ver El Video

(unamunoenlinea, 2012)
ARRIBA
|