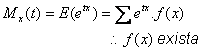3.5-Función Generadora de Momentos
|
Se llama función generadora de momentos (f.g.m), a la expresión: Mx(t) = E(e^tx), cuando este valor esperado existe para -b < t < b; donde b es numero real positivo. Para el caso de variables discretas se tiene que:
Y para variables continuas, así:
PROPIEDADES DE LA FUNCION GENERADORA DE MOMENTOS La importancia de la función generadora de momentos, radica en el hecho de que ella es única y determina completamente la distribución de una variable aleatoria, esto es, si dos variables aleatorias tienen una misma función Generatriz de momentos, deben tener igual distribución. La demostración de esta propiedad omitida en estos apuntes, se basa en la unidad que existe entre la f.g.m. y la función de distribución. La existencia de la función generatriz de momentos para -b<t<b, donde b es número positivo, garantiza la existencia de las derivadas de cualquier orden en t=0 .
(Quevedo Urías, 2006)
ASPECTOS A CONSIDERAR DE LA UNIDAD 3 Da Click En La Imagen Para Ver El Video (lasmatematicas.es, 2012)
|