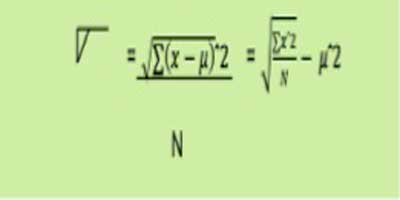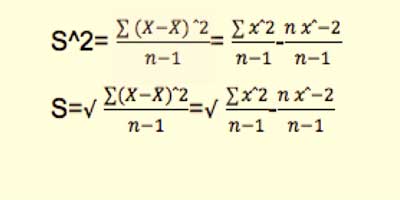1.3.-Medidas de Tendencia Central, de Dispersión, Simetría y Kurtosis

 MEDIDAS DE TENDENCIA CENTRAL

Las medidas de tendencia central conllevan información respecto al valor promedio de un conjunto de valores. Las tres medidas de tendencia central de uso más frecuente son: la media, la moda y la mediana.

1. MEDIA ARITMÉTICA: Para encontrar la media aritmética, sumamos los valores y resultados lo dividimos entre el número de observaciones o datos.

   DESVENTAJA: Los valores de los extremos afectan a los demás valores. 

MEDIA ARITMÉTICA PARA DATOS AGRUPADOS

Para encontrar la media aritmética de datos agrupados primero se calcula el punto medio de cada clase o intervalo (estos datos pueden ser redondeados) después multiplicamos cada punto medio por la frecuencia de observaciones de dicha clase, sumamos todos los resultados y dividimos esta suma entre el número total de observaciones de la muestra.

x = ∑ (f*x)

     n

x = Media aritmética para muestra

f = Frecuencia de los datos en la clase o intervalo

x = Punto medio de la clase

n = Número total de datos de la muestra

Figura 1.3.1 Ejemplificación de Símbolos

Ejemplo 1: Se presenta en la lista de aumento porcentual los resultados de un examen de admisión obtenidos por 7 estudiantes distintos que tomaron un determinado curso de preparación.

x=                ∑ x       Población

n

µ=                ∑ x          Muestra

N

Resultados de estudiantes

9

7

6

5

8

10

9

x=             ∑ x      = 7.7142         

            n

Ejemplo 2: La siguiente tabla muestra los saldos promedios mensuales de 600 cuentas de cheque.

x=            ∑ (f*x)       =  85350    =142.25

  N                600

2.  MEDIANA: Es el valor que queda en el centro de los datos, una vez que estos sean ordenados en forma ascendente o descendente. Para hallar la mediana de un conjunto de datos se organiza de forma progresiva; si el conjunto de datos contiene un número impar de elementos el elemento de en medio del arreglo es la mediana; si hay un número par de observaciones la mediana es el promedio aritmético de los elementos centrales. 

     Ejemplo: Hallar la mediana de los siguientes datos que muestraN el número de pacientes tratados en la sala de emergencias durante 8 días consecutivos; 52, 35, 43, 11, 30, 31, 86 y 49.

• • Ordenamos los datos: 11, 30, 31, 35, 43, 49, 52, 86

(35+43)/2= 78/2= 39

VENTAJAS DE LA MEDIANA:

1. • No se afecta por valores extremos.
   • Es fácil de entender
   • Se puede calcular a partir de cualquier tipo de datos (incluso en datos agrupados con extremo abierto)
   • Se puede hallar incluso cuando los datos son descripciones cualitativas.

DESVENTAJAS DE LA MEDIA:

1. • Ciertos procedimientos estadísticos que utiliza la mediana son más complejos que los que utiliza la media.
   • Como se tiene que ordenar los datos cuando más numerosos son estos implica, un valor consumo de tiempo.

3.    MODA: Es el valor que más se repite en un conjunto de datos.  Ejemplo: Hallar la moda del siguiente conjunto:

(2, 3, 3, 5, 3, 6, 9, 8, 5) = 3

      En el caso de los datos agrupados la moda está localizada en la clase que tiene la mayor frecuencia (a dicha clase se le llama clase modal). 

VENTAJAS DE LA MODA: 

1. 1. Se puede utilizar como una posición central para datos tanto cualitativos como cuantitativos.
   2. No se ve afectada por valores extremos, se puede obtener en datos agrupados aun cuando se tengan clases de extremo abierto.

DESVENTAJAS DE LA MODA:

1. 1. A menudo no existe un valor modal ya que los datos no se presentan más de una vez.
   2. Puede existir más de una moda y resulta difícil de interpretar.

NOTA: La media, la mediana y la moda, son idénticas en una distribución simétrica si solo hay una moda.

MEDIDAS DE DISPERSIÓN

La media de un conjunto de datos y las demás medidas de tendencia central indican el centro de una distribución de los datos, pero no proporciona en sí misma una descripción adecuada de un conjunto de mediciones. Dos conjuntos de mediciones podrían tener distribuciones de frecuencia muy distintas pero con la misma media, por eso para describir los datos de manera adecuada es preciso definir medidas de variabilidad de datos.

     La medida de variabilidad de más común empleada en estadística es la varianza, esta es útil para comparar la variación relativa de dos conjuntos de mediciones, pero solo cuando se interpreta en términos de desviación estándar proporciona información referente a la variación de un solo conjunto.

ALCANCE

(Rango o recorrido) El alcance es la diferencia entre el más alto y el más pequeño de los valores observados. Ejemplo: En el caso de la siguiente muestra hallar el alcance.

2, 3, 5, 2, 6, 9 y 8

El alcance es 7

NOTA: El alcance no nos da de ninguna información sobre lo que ocurre entre estos valores extremos y en consecuencia es de utilidad.

 DESVIACIÓN ESTÁNDAR

Es la raíz cuadrada de la varianza...

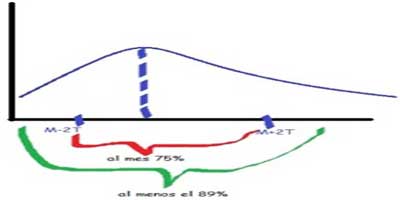
Figura 1.3.2 Fórmula Desviación Estándar 

     Esta, nos permite determinar con un buen grado de precisión donde están localizados lo valores de una distribución de frecuencias con relación a la media, se puede hacer de acuerdo al teorema de CHEBY SHEV,  no importa que forma tenga la distribución, al menos el 75% de los valores caen dentro de ±2 √ a partir de la media de distribución y al menos 89% de los valores caen dentro de más  menos ±3√.

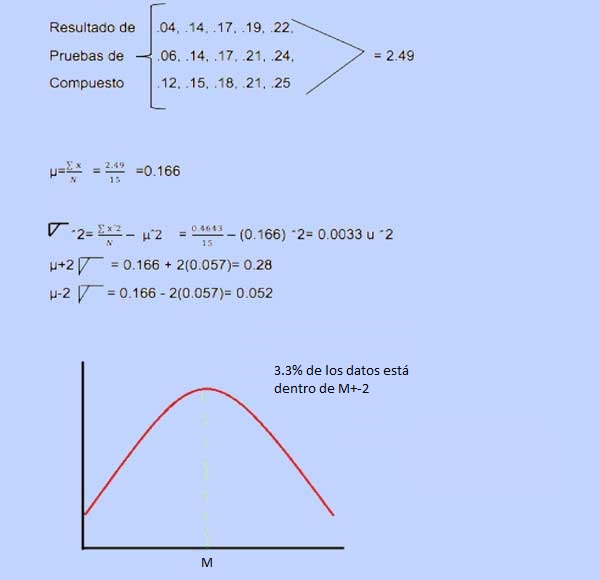
Figura 1.3.3 Uso de la Desviación Estándar

     Ejemplo:Considere la siguiente tabla que muestre una población de 15 frascos de compuesto producido en un día donde se determinó la pureza de este, determine la media de varianza y la desviación estándar además determine entre que valores están al menos el 75% de los datos.

Porcentaje de impureza observada.

Figura 1.3.4 Desviación Estándar Aplicada a la Pureza de los frascos

VARIANZA Y DESVIACIÓN ESTÁNDAR PARA MUESTRA

Figura 1.3.5 Fórmulas de Varianza y Desviación Estándar

sˆ2= Varianza de la muestra

s= Desviación estándar de la muestra

     Ejemplo: Dada la siguiente lista de asistencia de un grupo de francés, encontrar la media, la mediana, la varianza y la desviación estándar, además determine entre que valores esta el 75% de los datos.

1, 2, 4, 2, 4, 3, 2, 1, 5, 7,

8, 9, 1, 3, 4, 5, 7, 8, 9, 1,

3, 4, 5, 7, 6, 2, 1, 3, 4, 9,

8, 1, 3, 2, 1, 7, 2, 3, 4, 5,

3, 4, 3, 4, 1, 2, 7, 8, 9, 5,

1, 2, 3, 4, 7, 6, 8, 9, 1, 5,

6, 3, 2, 4, 7, 6, 8, 9, 3, 4.

µ= (310/70) =4.428 ->media

Mediana= 4

Moda= 3 y 4

111111111222222223333333333444444444445555566667777777888888999999

Figura 1.3.6 Cálculo de Varianza y Desviación Estándar  

SESGO Y KURTOSIS

• SESGO: Las curvas que representan los datos de un conjunto pueden ser simétricas o sesgadas.Las curvas simétricas tienen una curva tal que una línea vertical que pase por el punto más alto de la curva dividirá el área en dos partes iguales. En una curva sesgada de distribución de puntos está concentrada en un extremo u otro. La primera curva que se muestra es una curva simétrica y las dos siguientes sesgadas.

• KURTOSIS: Es el lado de agudeza de una distribución de datos.

(Machado P., 2011)

ASPECTOS A CONSIDERAR DE LA UNIDAD 1

 Da Click En La Imagen Para Ver El Video

(Canal, 2012)

ARRIBA