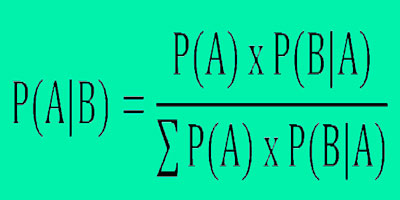2.4-Teoremas de Probabilidad Total y de Bayes

TEOREMA DE PROBABILIDAD TOTAL

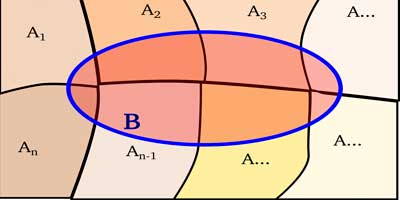
El siguiente teorema denominado teorema probabilidad total o regla de eliminación permite hallar la probabilidad de un evento A cuando el espacio muestral S sea dividido en varios eventos B1,B2,B3,… hasta Bx.

     Si los eventos B1, B2, B3….Bk constituyen una división muestral del espacio S de tal forma que la probabilidad de Bi ≠ 0 para i=1,2,3, …, k, entonces, para cualquier evento A en S se tiene lo siguiente.

P (A) = ∑^k _i=1 P (Bi) * P (A)(Bi) = ∑^k _i=1  P (A n Bi)

r=3

i= 1, 2, 3

Figura 2.4.1 Teorema de Probabilidad Total

     Si en lugar de querer la probabilidad de A  como lo menciona el Teorema de Probabilidad Total, se desea la probabilidad condicional de P(Br|A), entonces se aplica el siguiente Teorema...

TEOREMA DE BAYES

Si los eventos B1, B2, B3….Bk constituyen una división muestral del espacio S donde P(Bi) ≠ 0 para i=1,2,3, …, k, entonces, para cualquier evento A en S tal que la probabilidad de A sea diferente de cero, se tiene lo siguiente.

 Figura 2.4.2 Teorema de Bayes

EJEMPLO 1

En la sala de pediatría de un hospital, el 60% de los pacientes son niñas. De los niños el 35% son menores de 24 meses. El 20% de las niñas tienen menos de 24 meses. Un pediatra que ingresa a la sala selecciona un infante al azar.

a. Determine el valor de la probabilidad de que sea menor de 24 meses.

b. Si el infante resulta ser menor de 24 meses. Determine la probabilidad que sea una niña.

SOLUCIÓN:

Se definen los sucesos:

Suceso H: seleccionar una niña.

Suceso V: seleccionar un niño.

Suceso M: infante menor de 24 meses.

En los ejercicios de probabilidad total y teorema de bayes, es importante identificar los sucesos que forman la población y cuál es la característica que tienen en común dichos sucesos. Estos serán los sucesos condicionados.

1. En este caso, la población es de los infantes. Y la característica en común es que sean menores de 24 meses. Por lo tanto, la probabilidad de seleccionar un infante menor de 24 meses es un ejemplo de probabilidad total. Su probabilidad será: P(M) =P(H) * P(M|H) + P(V) * P(M|V) =(0.6* 0.2) + (0.4* 0.35) = 0.26 ó 26%

1.  Para identificar cuando en un ejercicio se hace referencia al teorema de bayes, hay que partir de reconocer que esta es una probabilidad condicionada y que la característica común de los sucesos condicionantes ya ha ocurrido. Entonces, la probabilidad de que sea niña una infante menor de 24 meses será:  P(H|M)=( P(H) * P(M|H) ) / ( P(H) * P(M|H) + P(V) * P(M|V)) = (0.6* 0.2) / ((0.6* 0.2 )+ (0.4*0.35)) = 0.12/ 0.26 = 0.46 ó 46%

(E. Walpole, H. Myers, & L. Myers, 2012)

ARRIBA