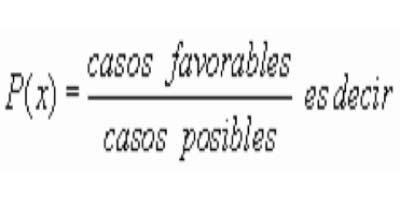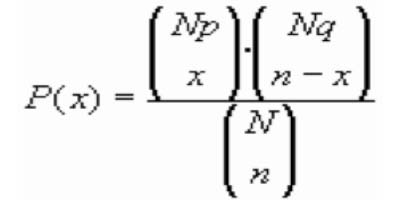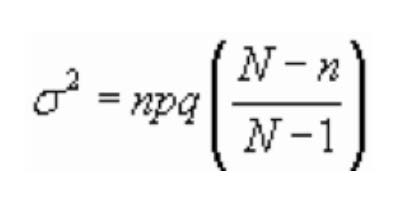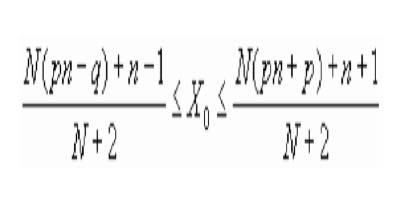4.2-Hipergeométrica e Hipergeométrica Multivariada
| HIPERGEOMÉTRICA Hasta ahora hemos analizado distribuciones que proporcionan situaciones en las que se realizaban pruebas que entrañaban una dicotomía (proceso de Bernouilli) de manera que en cada experiencia la probabilidad de obtener cada uno de los dos posibles resultados se mantenía constante. Si el proceso consistía en una serie de extracciones o selecciones ello implicaba la reposición de cada extracción o selección , o bien la consideración de una población muy grande. Sin embargo si la población es pequeña y las extracciones no se remplazan las probabilidades no se mantendrán constantes . En ese caso las distribuciones anteriores no nos servirán para la modelizar la situación. La distribución hipergeométrica viene a cubrir esta necesidad de modelizar procesos de Bernouilli con probabilidades no constantes (sin reemplazamiento) . La distribución hipergeométrica es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realizan experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial. Modeliza , de hecho, situaciones en las que se repite un número determinado de veces una prueba dicotómica de manera que con cada sucesivo resultado se ve alterada la probabilidad de obtener en la siguiente prueba uno u otro resultado. Es una distribución .fundamental en el estudio de muestras pequeñas de poblaciones .pequeñas y en el cálculo de probabilidades de, juegos de azar y tiene grandes aplicaciones en el control de calidad en otros procesos experimentales en los que no es posible retornar a la situación de partida. La distribución hipergeométrica puede derivarse de un proceso experimental puro o de Bernouilli con las siguientes características: El proceso consta de n pruebas , separadas o separables de entre un conjunto de N pruebas posibles. Cada una de las pruebas puede dar únicamente dos resultados mutuamente excluyentes: A y no A. En la primera prueba las probabilidades son : P(A)= p y P(A)= q ; con p + q = l. Las probabilidades de obtener un resultado A y de obtener un resultado no A varían en las sucesivas pruebas, dependiendo de los resultados anteriores. Derivación de la distribución: Si estas circunstancias aleatorizamos de forma que la variable aleatoria X sea el número de resultados A obtenidos en n pruebas la distribución de X será una Hipergeométrica de parámetros N, n, p así X -> H (N, n, p) Un típico caso de aplicación de este modelo es el siguiente: Supongamos la extracción aleatoria de n elementos de un conjunto formado por N elementos totales, de los cuales Np son del tipo A y Np son del tipo ‾A(p + q = l). Si realizamos las extracciones sin devolver los elementos extraídos , y llamamos X. al número de elementos del tipo A que extraemos en n extracciones X seguirá una distribución hipergeométrica de parámetros N , n , p. FUNCIÓN DE CUANTÍA La función de cuantía de una distribución Hipergeométrica hará corresponder a cada valor de la variable X (x = 0,1,2, . . . n) la probabilidad del suceso "obtener x resultados del tipo A ", y (n-x) resultados del tipo no A en las n pruebas realizadas de entre las N posibles. Veamos :
Hay un total de
Por otro lado si realizamos n pruebas o extracciones
hay un total de
Figura 4.2.1 Función de Cuantía Que para valores de X comprendidos entre el conjunto de enteros 0,1,…. .n será la expresión de la función de cuantía de una distribución , Hipergeométrica de parámetros N, n, p. MEDIA Y VARIANZA Considerando que una variable hipergeométrica de parámetros N, n, p puede considerarse generada por la reiteración de un proceso dicotómico n veces en el que las n dicotomías NO son independientes ; podemos considerar que una variable hipergeométrica es la suma de n variables dicotómicas NO independientes. Es bien sabido que la media de la suma de variables aleatorias (sean éstas independientes o no) es la suma de las medias y por tanto la media de una distribución hipergeométrica será , como en el caso de la binomial : En cambio si las variables sumando no son independientes la varianza de la variable suma no será la suma de las varianzas. Si se evalúa el valor de la varianza para nuestro caso se obtiene que la varianza de una distribución hipergeométrica de parámetros N, n, p es : si X -> H (N, n, p)
Figura 4.2.2 Fórmula de Varianza Esta forma resulta ser la expresión de la varianza de una binomial (n, p) afectada por un coeficiente corrector [N-n/N-1], llamado coeficiente de exhaustividad o Factor Corrector de Poblaciones Finitas (F.C.P.F.) y que da cuenta del efecto que produce la no reposición de los elementos extraídos en el muestreo. Este coeficiente es tanto más pequeño cuanto mayor es el tamaño muestral (número de pruebas de n ) y puede comprobarse como tiende a aproximarse a 1 cuando el tamaño de la población N es muy grande . Este último hecho nos confirma lo ya comentado sobre la irrelevancia de la reposición o no cuando se realizan extracciones sucesivas sobre una población muy grande. Con una población muy grande se cual fuere el tamaño de n , el factor corrector sería uno lo que convertiría , en cierto modo a la hipergeométrica en una binomial (ver D. Binomial) . Así
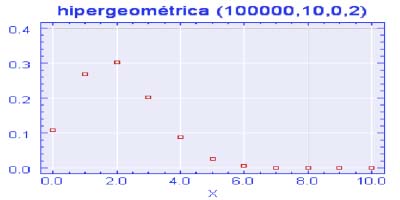
Hemos visto como la media de la distribución hipergeométrica [ H ( N, n, p ) ], tomaba siempre el mismo valor que la media de una distribución binomial [ B ( n, p ) ] también hemos comentado que si el valor del parámetro N crecía hasta aproximarse a infinito el coeficiente de exhaustividad tendía a ser 1, y, por lo tanto, la varianza de la hipergeométrica se aproximaba a la de la binomial : puede probarse asimismo , cómo la función de cuantía de una distribución hipergeométrica tiende a aproximarse a la función de cuantía de una distribución binomial cuando N->∞ Puede comprobarse en la representación gráfica de una hipergeométrica con N =100000 como ésta ,es idéntica a la de una binomial con los mismos parámetros restantes n y p , que utilizamos al hablar de la binomial.
Figura 4.2.3 Gráfica de la distribución hipergeométrica De manera análoga a como se obtenía la moda en la distribución binomial es fácil obtener la expresión de ésta para la distribución hipergeométrica. De manera que su expresión X0 sería la del valor o valores enteros que verificasen.
Figura 4.2.4 Moda de la distribución hipergeométrica
HIPERGEOMÉTRICA MULTIVARIADA Justo como la distribución hipergeométrica toma el lugar de distribución binomial para el muestreo sin reemplazo, también existe una distribución multivariada análoga a la distribución multinomial que aplica al muestreo sin reemplazo. Para derivar esta formula, consideremos un conjunto de N elementos, de los cuales M1, son elementos de la primera clase, M2 son elementos de la segundo clase …. y Mk son elementos de la k-esima clase tales que.
Figura 4.2.5 Fórmula Hipergeométrica Multivariada Como en relación con la distribución multinomial, estamos interesados en la probabilidad de obtener X1 elementos (resultados) de la primera clase, X2 elementos de la segunda clase …. y Xk elementos de la k-esima clase, pero ahora estamos escogiendo sin reemplazo, n de los N elementos del conjunto.
Hay
Figura 4.2.6 Distribución Hipergeométrica Multivariada Así la distribución conjunta de las variables aleatorias bajo consideración, esto es, la distribución de los números de resultados de la diferentes clases, es una distribución hipergeométrica multivariada con los parámetros n, M1, M2, … y Mk.
(Cedeño, 2013)
|
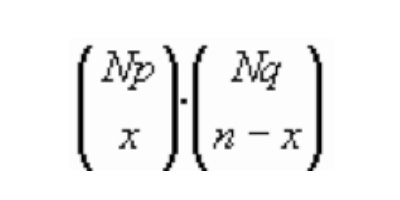 formas distintas
de obtener x resultados del tipo A y n-x del tipo ‾A ,
si partimos de una población formada por Np elementos
del tipo A y Nq elementos del tipo ‾A.
formas distintas
de obtener x resultados del tipo A y n-x del tipo ‾A ,
si partimos de una población formada por Np elementos
del tipo A y Nq elementos del tipo ‾A.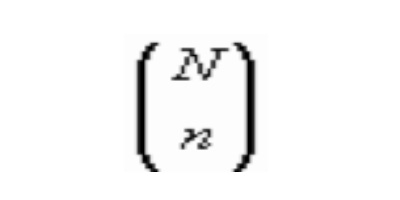 posibles muestras
( grupos de n elementos) aplicando la regla de Laplace
tendríamos:
posibles muestras
( grupos de n elementos) aplicando la regla de Laplace
tendríamos: