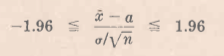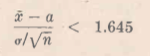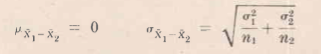7.2-Relacionadas con Medias
|
Pruebas de Hipótesis de Significación para grandes Muestras Para muestras grandes, las distribuciones muéstrales de muchos estadísticos son distribuciones normales(o al menos casi normales) con media μs y desviación típica σs. Aquí S = X,la media muestral; μs = μx = μ media poblacional; σs=σx=σ/√n donde σ es la desviación típica poblacional y n es el tamaño de la muestra. La variable tipificada viene dada por: Z= ( x-μ )/(σ/√n) Para ensayar la hipótesis nula H0 de que la media poblacional es μ = α utiliza¡íamos un ensayo de dos colas, aceptando H0 (o al menos no rechazándolo) al nivel 0.05. Figura 7.2.1 Muestra Específica de Tamaño n con Media x. y lo rechazaríamos por el contrario. Para otros niveles de significación cambiaríamos apropiadamente. Para ensayar la hipótesis de que la media poblacional es mayor α, utilizamos aun la hipótesis nula H0 de que es igual a α. Entonces, utilizando un ensayo de una cola, aceptaríamos H0 (o al menos no la rechazaríamos) al nivel 0.05 si
Figura 7.2.2 Muestra Específica de Tamaño n con Media x.
Diferencias de Medias Sean X1 y X2 las medias muestrales obtenidas en dos muestras grandes de tamaño n1 y n2 extraídas de poblaciones respectivas que tienen de medias μ1 y μ2 desviaciones típicas σ1 y σ2. Considérese la hipótesis nula de que no hay diferencia entre las medias poblacionales, es decir, μ1 = μ2, se ve que la distribución muestral de la diferencia de medias se distribuye aproximadamente como una normal con media y desviación típica dadas por: Figura 7.2.3 Distribución Muestral de Diferencia de Medias.
(Murray R., 1976) |