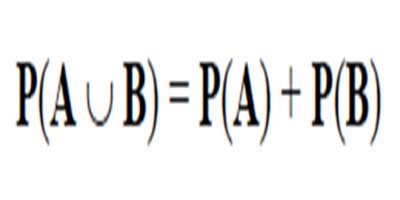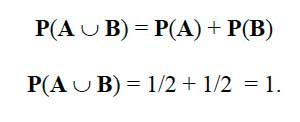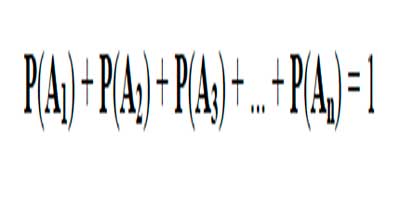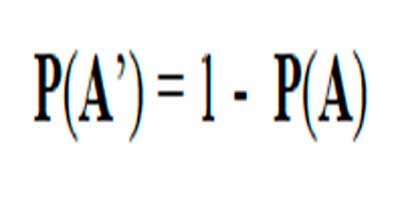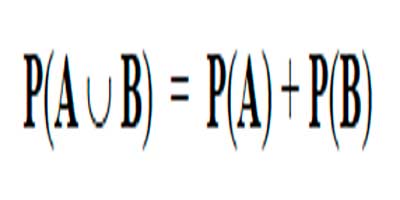2.1.-Definición, Axiomas y Teoremas
|
La probabilidad indica el grado de certidumbre o certeza de un suceso o fenómeno estudiado, en la investigación científica existen muchos fenómenos en los cuales es necesario determinar la probabilidad de que un evento(s) ocurra(n) o dejen de ocurrir, para lo cual el estudio de este campo, es necesario, además tiene aplicaciones muy importantes en investigación; dado que es base para la inferencia estadística que permite el estudio de muestras con el objetivo de inferir o extrapolar características de estas a una población. (Hanke John E & Arthur Reitsch, 1997)
AXIOMAS Un axioma es el elemento básico de un sistema de lógica formal y junto con las reglas de inferencia definen un sistema deductivo. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba. La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre esta otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y sólo de ellos, han de deducirse todas las demás proposiciones de la teoría dada. Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos. Los axiomas de la formulación moderna de la teoría de la probabilidad constituyen una base para deducir a partir de ellas un amplio número de resultados. La letra P se utiliza para designar la probabilidad de un evento, siendo P(A) la probabilidad de ocurrencia de un evento A en un experimento.
AXIOMA 1: Si A es un evento de S, entonces la probabilidad del evento A es:
Figura 2.1.1 Probabilidad De Evento A
Como no podemos obtener menos de cero éxitos ni más de n éxitos en n experimentos, la probabilidad de cualquier evento A, se representa mediante un valor que puede variar de 0 a 1.
AXIOMA 2: Si dos eventos son mutuamente excluyentes, la probabilidad de obtener A o B es igual a la probabilidad de obtener A más la probabilidad de obtener B.
Figura 2.1.2 Eventos Mutuamente Excluyentes
Excluirse mutuamente quiere decir que A y B no pueden ocurrir simultáneamente en el mismo experimento. Así, la probabilidad de obtener águila o sol en la misma tirada de una moneda será:
Figura 2.1.3 Propiedades De La Exclusión
En general podemos decir que la suma de las probabilidades de todos los posibles eventos mutuamente excluyentes es igual a 1:
Figura 2.1.4 Suma De Eventos Mutuamente Excluyentes
AXIOMA 3: Si A es un evento cualquiera de un experimento aleatorio y A’ es el complemento de A, entonces:
Figura 2.1.5 Propiedades Del Axioma 3
Es decir, la probabilidad de que el evento A no ocurra, es igual a 1 menos la probabilidad de que ocurra.
(Lipschutz S., 1971)
TEOREMAS Suponiendo que P(A) y P(B) representan las probabilidades para los dos eventos A y B, entonces P(A U B) significa la probabilidad de que ocurran A o B. Si representamos los eventos A y B en un Diagrama de Venn con:
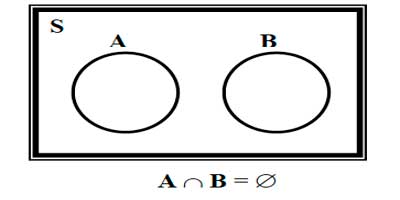
Figura 2.1.6 Representación de Los Eventos A y B en un Diagrama de Venn
Entonces A y B son conjuntos disjuntos o mutuamente excluyentes, o sea que no pueden ocurrir en forma simultánea
Figura 2.1.7 Fórmula Para La Union De A y B
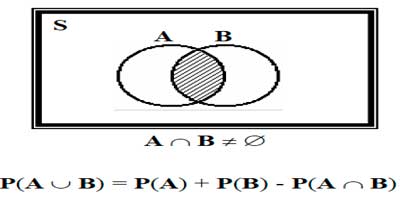
En cambio, si ambos eventos tienen puntos muestrales en común
Figura 2.1.8 Representación De la Interacción Entre A y B ( Mason R & Douglas Lind, 1990)
|