Función

Una función ƒ de un conjunto D a un conjunto E es una correspondencia que asigna exactamente un elemento y de E a cada elemento x de  D.

El elemento x de D es el argumento de ƒ. El conjunto D es el dominio de la función. El elemento y de E es el valor de ƒ en x (o la imagen de x bajo ƒ) y se denota con ƒ(x), que se lee "ƒ de x". La imagen de ƒ es el subconjunto R de E formado por todos los valores posibles ƒ(x) para x en D.

Los símbolos

                y       

significan que ƒ es una función de D a E, y decidimos que ƒ transforma a D en E. 

Dos funciones ƒ y g de D a E son iguales y escribimos:

ƒ = g siempre que ƒ(x) = g(x) para toda x en D.

Ejemplo:

Sea ƒ la función con dominio tal que ƒ(x)=x² para toda x en .

(a) Encuentra ƒ(-6), ƒ(√3), ƒ(a+b) y ƒ(a) + ƒ(b), donde a y b son números reales.

(b) ¿Cuál es la imagen de ƒ?

Solución:

(a) Encontramos valores de ƒ al sustituir x en la ecuación ƒ(x)=x².

ƒ(-6) = (-6)²= 36

ƒ(√3) = (√3)² = 3

ƒ(a + b) = (a + b)² = a² + 2ab + b²

ƒ(a) + ƒ(b) = a² + b²

(b) Por definición, la imagen de ƒ está formado por todos los números de la forma ƒ(x)=x² para x en . En vista de que el cuadrado de todo número real es no negativo, el intervalo está contenido en el conjunto de todos los números reales no negativos.

Gráfica de una función

La gráfica de una función ƒ es la gráfica de la ecuación y = ƒ (x) para x en el dominio de ƒ.

Con frecuencia colocamos la leyenda y = ƒ (x) en un dibujo de la gráfica. Si P(a,b) es un punto de la gráfica, la coordenada y igual a b es el valor de función ƒ(a).

Ejemplo:

Sea ƒ(x) = √x-1

1. Traza la gráfica de ƒ.
2. Encuentra el dominio y la imagen de ƒ.

Solución

1. Por definición, la gráfica de ƒ es la gráfica de la ecuación y = √x-1. La tabla siguiente enumera las coordenadas de varios puntos de la gráfica.

Al trazar los puntos se obtiene: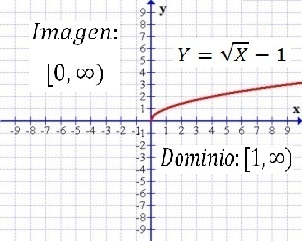

Observando que la abscisa al origen es 1 y no hay ordenada al origen.

2. Al observar la gráfica, podemos ver que el dominio de ƒ está formado por todos los números reales x tales que x ≥ 1 o, lo que es equivalente, el intervalo [1,∞). La imagen de ƒ es el conjunto de todos los números reales y tales que y ≥ 0 o, lo que es equivalente, [0, ∞) .