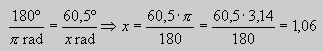Una circunferencia se determina cuando conocemos los tres principales puntos, equidistantes del centro.

• El centro y el radio.
• El centro y un punto en ella.
• El centro y una recta tangente a la circunferencia.

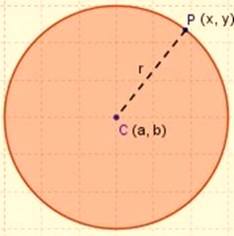
También podemos decir que la circunferencia es la línea formada por todos los puntos que están a la misma distancia de otro punto, llamado CENTRO.

Esta propiedad es la clave para hallar la expresión de una circunferencia (Ecuación de la circunferencia).

Ahora explicaremos dentro del Plano Cartesiano. Se deduce que para cualquier punto, P (x, y),  de una circunferencia cuyo centro  es el punto C (a, b) y con radio r, la ecuación ordinaria es

(x ─ a)² + (y ─ b)² = r²

 

Esto significa que una circunferencia graficada con un centro definido (coordenadas) en el plano Cartesiano y con radio conocido la podemos “ver” como gráfico y también la podemos “transformar” o expresar como una ecuación matemática.

 

Recordar siempre que en esta fórmula la x y la y serán las coordenadas de cualquier punto (P) sobre la circunferencia, equidistante del centro un radio (r). Y que la a y la b (o la h y la k, según se use) corresponderán a las coordenadas del centro de la circunferencia C(a, b).

 

Radianes

 

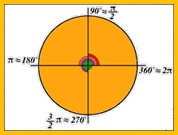
Los grados sexagesimales, se emplean para dividir  la circunferencia en 360 partes iguales. Si colocamos el eje de coordenadas en la circunferencia tendremos que éste coincide con el 90, 180, 270 y 360 grados.

 

Otra de las medidas de ángulos más utilizada en trigonometría es el RADIÁN

Por tanto, el ángulo, α, completo en radianes de una circunferencia de radio, r, sería:

 

 

 

 

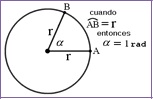
Su símbolo es rad.

 

 

 

La equivalencia entre grados y radianes la podemos observar en la circunferencia, y calcular para cualquier ángulo:

 

 

Despejamos y obtenemos que: