1.6.1 Conocimientos Previos de Geometría Plana
|
Definición 1: Sea L una recta de ecuación y = mx + b, con m ∈ R, b ∈ R. Si A y B son puntos de L, entonces escribimos L = ←A−−→B
La recta L la podemos representar geométricamente sin usar coordenadas rectangulares de la siguiente forma:
Definición 2
Sea L una recta de ecuación y = mx + b, con m ∈ R, b ∈ R y sean A, B y C tres puntos en L como se muestra en la siguiente figura:
Sea B = (x0 , y0 ). Los conjuntos definidos por:
a.) −B−→A = {(x, y) ∈ L/ x ≤ x0 }
b.) −B−→C = {(x, y) ∈ L/ x ≥ x0 }
Reciben el nombre de rayos y el punto B recibe el nombre de origen o punto inicial del rayo. De acuerdo con la figura anterior, los rayos −B−→A y −B−→C se pueden representar respectivamente así:
Definición 3
Círculo. Sea P un plano, O un punto en P y r ∈ R, r ≥ 0. Se llama círculo de centro O y de radio r, al conjunto de puntos en P cuya distancia a O es r.

Ejemplo 1:
a) Sea C un círculo cuyo radio es 2cm y su centro es el punto (0, 0), entonces C se puede representar así.

Ejercicios:
Represente cada uno de los siguientes círculos
1. C es un círculo de radio 3, 5cm y su centro es (−2, −1)
2. C es un círculo de radio 4cm y su centro es (0, 2)
3. C es un círculo de radio 2, 25cm y su centro es (−3, 2)
Definición 4
Ángulo plano. Se llama ángulo plano a la unión de dos rayos con un origen común. Los rayos que forman un ángulo se llaman lados del ángulo y al punto común u origen de los rayos, se llama vértice del ángulo.
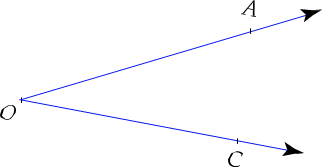
En la figura anterior los rayos −O→A y −O−→C determinan un ´angulo y se denota LAOC (LAOC se lee “´angulo AOC ”) |