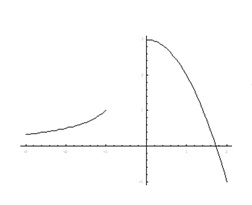
Dominio

Si la función está dada por una gráfica,  el dominio se puede determinar viendo cuál es el intervalo o intervalos de x entre los que existe función:

En esta gráfica vemos que la función está definida para valores de x que van

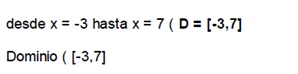
Puede que la función esté definida en intervalos separados o disjuntos; en este caso, el dominio es la unión de los distintos intervalos en los que exista dibujo de gráfica.

Como ya vimos, EL DOMINIO de una función es el conjunto de valores para los cuales la función está definida; es decir,  son todos los valores que puede tomar la variable independiente (la x).

Por ejemplo:

La función f(x) = 3x² – 5x está definida para todo número real (x puede ser cualquier número real).

Así EL DOMINIO de esta función es el conjunto de todos los números reales.
En cambio, la función   

Tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.

Si el dominio no se específica, debe entenderse que el dominio incluye a todos los números reales para los cuales la función tiene sentido.

En el caso de la función 

El dominio de esta función son todos los números reales mayores o iguales a –3, ya que  x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.

• Si la función tiene radicales de índice par, el dominio está conformado por todos los números reales para los cuales la cantidad subradical sea mayor o igual a cero.
• Si la función es un polinomio; una  función  de  la  forma   f(x) = a₀ + a₁x + a₂x² +...+ a_nxⁿ (donde a₀, a₁, a₂,..., a_n son constantes y n un entero no negativo), el dominio está conformado por el conjunto de todos los números reales.
• Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.
• El rango (recorrido o ámbito) es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.

Ejemplo:      

Identificar dominio y rango de la función  

Solución:

Como la función tiene radicales el dominio está conformado por todos los valores para los cuales  x – 2 ≥ 0. Esto es, el dominio de la función incluye todos los reales que son mayores o iguales a 2.

El rango es igual al conjunto de los números reales positivos incluyendo el cero; puesto que al reemplazar los valores del dominio se obtienen únicamente valores positivos bajo la función f.