1.1 Números Reales
|
Se conoce que desde la antigüedad, de acuerdo con pinturas rupestres, jeroglíficos, pergaminos, entre otros, que el concepto de número surgió por la necesidad práctica de contar objetos, inicialmente se contaba con la ayuda de los medios disponibles: dedos, piedras, nudos, marcas, posteriormente debido a la agrupación de objetos con características semejantes surge el concepto de conjunto, el cual se utilizó para realizar sumas, restas en forma gráfica, lo que permitió crear las bases para la creación de las operaciones aritméticas, dando origen a la palabra cálculo que se deriva de la palabra latina calculus, que significa ”contar con piedras”. Los números surgen por necesidades sociales, para calcular y medir cantidades de objetos para diversas indoles.
Para Isaac Newton, es la relación abstracta entre una magnitud cualquiera y otra del mismo genero tomada por nosotros como unidad.
Números Reales Los números reales son aquellos que pueden ser expresados por un número entero o decimales o la combinación de éstos, ya sea positivo o negativo. El conjunto de los números reales está compuesto a su vez por los conjuntos de números naturales, enteros, racionales e irracionales, como se observa en la figura.
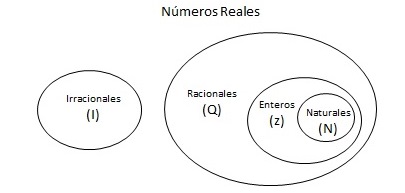
Números Naturales (N). Los números 0, 1,2,3,4 .. que usamos tan frecuentemente en nuestra vida diaria, reciben el nombre de números naturales, son el primer conjunto de números que el hombre utiliza, generalmente para indicar la cantidad de objetos que tiene un conjunto. Se inicia con el número cero, es decir: N = {0,1,2,3,4,5,6,7,8,9,10,11…..} X {x / x є N} Número Enteros (Z). Se definen como un número que no tiene parte fraccionaria (o decimal),está formado por el conjunto de los números positivos y negativos, incluyendo el cero. Z = { … -4, -3, -2, -1, 0 , 1, 2, 3, 4, … } x {x / x є Z} Números Racionales (Q). Se definen como aquellos números que pueden ser expresados por la división de dos enteros. Q= { x = a/b a є Z y b є Z} {x/x є Q} Ejemplo: ¾, ½ , 1.3333… 143.5 Número Irracionales (I)
Son aquellos números que no se pueden escribir como la división de dos enteros. Ejemplo: √2, √3 , √5, ℮, ¶
En la siguiente imagen se muestra la clasificación de los números.
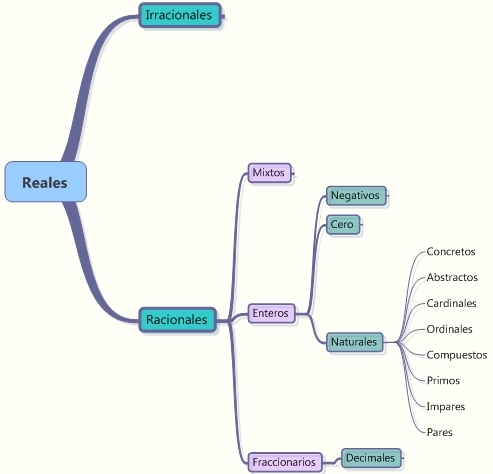
|