1.6.2 Medida de Ángulos
|
Para medir ángulos existen dos sistemas de medición uno que usa como unidad de medida el grado, y otro que usa como unidad de medida el radián. |
||||||||||||||||||||||||
|
Medida en grados
Consideremos el LABC como ángulo central de un círculo
y con sentido positivo.
Se dice que la medida del LABC es un grado (1◦ ) si subtiende un arco cuya medida es 1/360 de la circunferencia.

Notación: m LABC = 1◦ ; m LABC se lee “medida del ´ángulo ABC ”
Algunos ejemplos de la representación de ángulos
Medida en radianesPara definir lo que entenderemos por radián estudiaremos los arcos del círculo así como su medición y tomar como referencia que los círculos de radio uno tienen como circunferencia 2π.
Sea C un círculo de radio 1 y centro en el origen del sistema de coordenadas rectangulares
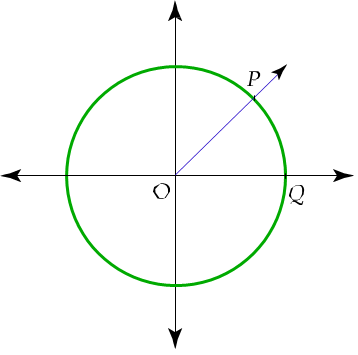
Diremos que el valor absoluto de la medida
del LP OQ, en radianes, es igual a la longitud
del arco P Q
Nota:
1. Si un ángulo ha sido engendrado por rotación positiva, entonces se le asigna una medida positiva.
2. Si un ángulo ha sido engendrado por rotación negativa, entonces se le asigna una medida negativa.
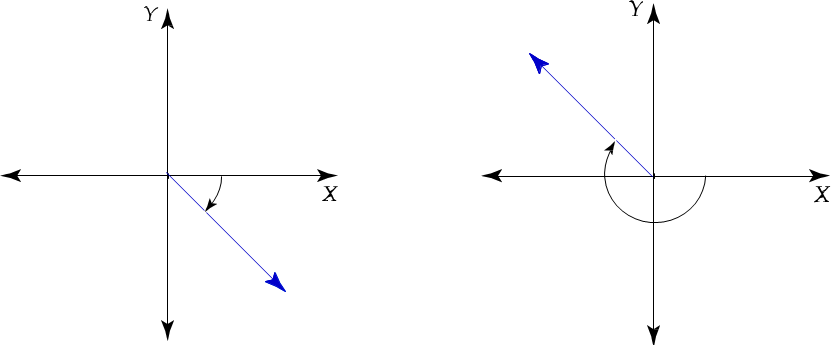
Los ángulos que se representan a continuación tienen medida negativa.
|