2.3.1 Algebraicas
|
Función Lineal Una función ƒ es una función lineal si ƒ(x) = ax + b, donde x es cualquier número real y a y b son constantes. La gráfica de ƒ es la gráfica de y = ax + b, que, por la forma pendiente-intersección, es una recata con pendiente a y ordenada al origen igual a b; por lo tanto, la gráfica de una función lineal es una recta. 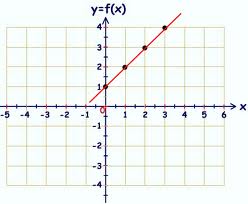
Función Cuadrática Una función ƒ es cuadrática si ƒ(x) = ax2 + bx + c, donde a,b,c son números reales con a ≠ 0. Si b = c = 0, entonces ƒ (x) = ax2 y la gráfica es una parábola con vértice en el origen. si b = 0 y c ≠ 0, entonces: ƒ (x) = ax2 + c por lo tanto la gráfica es una parábola con vértice en el punto (0, c) en el eje de las y. 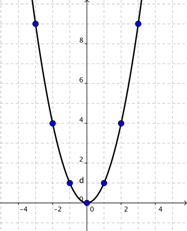
Función Cúbica Una función ƒ es cúbica si ƒ(x) = ax3 + bx2 + cx + d 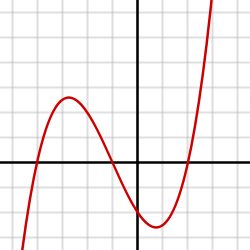
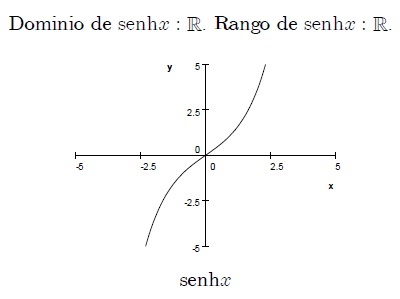
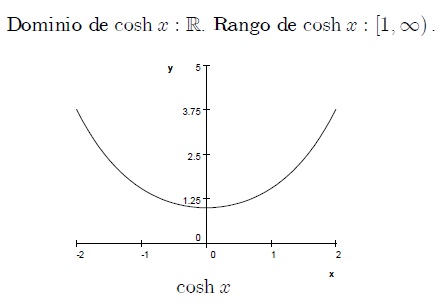
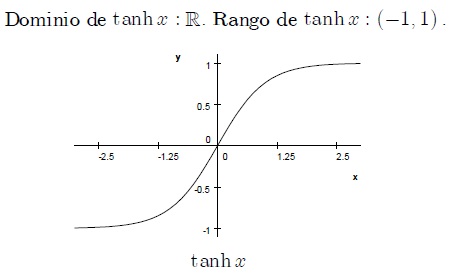
Función Hiperbólica Se llaman funciones hiperbólicas, por que de alguna manera tienen propiedades similares a las funciones trigonométicas y se relacionan con la hipérbola en la forma en la que las funciones circulares se relacionan con el circulo. 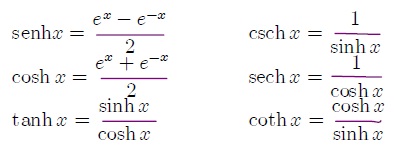
Operaciones de funciones Sean ƒ y g dos funciones que van de los Reales a los Reales y cuyos dominios son respectivamente Df y Dg. Se definen las cuatro operaciones fundamentales de la siguiente manera:
El dominio de la suma, diferencia, producto y cociente denotado por Df + g, Df - g, Dfg, Df/g respectivamente, se define por:
|