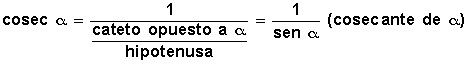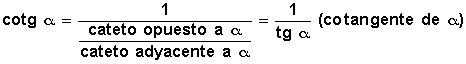1.6.4 Las Funciones Trigonométricas Seno y Coseno
|
Sea P un punto en el círculo trigonométrico, tal que P = (x, y), sea α la medida del ángulo formado por la parte positiva del eje X y el rayo OP Se definen las funciones:
coseno : R −→ R α −→ x, o sea, coseno(α) = x
seno : R −→ R α −→ y, o sea, seno(α) = y
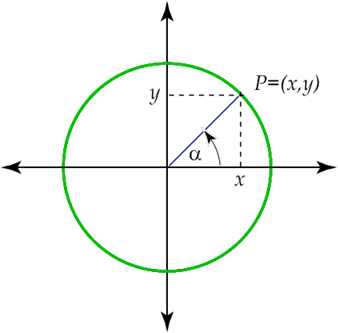
Por lo anterior se obtiene que x = cos(α); y = sen(α) o sea, P = (x, y) = (cos (α), sen (α))
· Seno: Se obtiene dividiendo el cateto opuesto entre la hipotenusa. · Coseno: Se obtiene dividiendo el cateto adyacente entre la hipotenusa. · Tangente: Se obtiene dividiendo el cateto opuesto entre el cateto adyacente. · Cotangente: Se obtiene dividiendo el cateto adyacente entre el cateto opuesto. · Secante: Se obtiene dividiendo la hipotenusa entre el cateto adyacente. · Cosecante: Se obtiene dividiendo la hipotenusa entre el cateto opuesto.
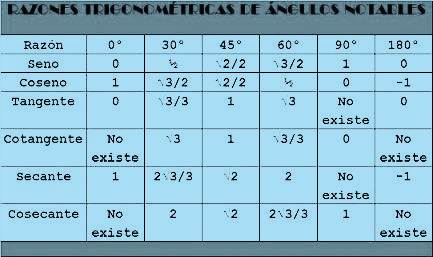
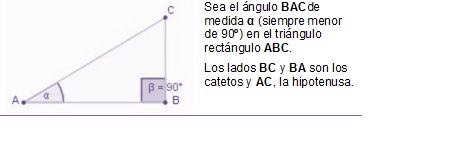
Para establecer las razones trigonométricas, en cualquier triángulo rectángulo, es necesario conocer sus elementos:
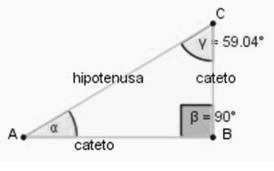
Los ángulos con vértice en A y C son agudos, el ángulo con vértice en B es recto. El triángulo rectángulo se caracteriza por que los lados de los ángulos agudos (α y γ) son la hipotenusa y un cateto, y los lados del ángulo recto (β) son los catetos. Cada uno de los ángulos águdos del triángulo, uno de cuyos lados es la hipotenusa, se relaciona con los catetos, que pueden ser cateto opuesto al ángulo o cateto adyacente al ángulo.
Con los siguientes ejemplos, veamos lo dicho:
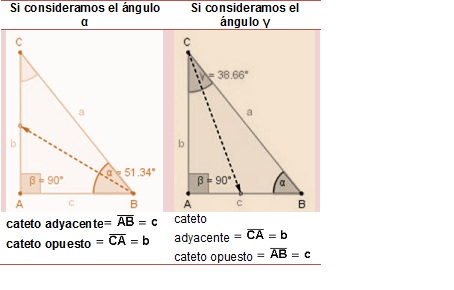
Las razones o relaciones trigonométricas se establecen entre dos lados de un triángulo rectángulo en relación con cada uno de sus ángulos agudos. También se llaman Funciones trigonométricas.
En este triángulo rectángulo, las razones trigonométricas con respecto a alfa (α) se definen como: Seno
Seno, es la razón (división) entre el cateto opuesto al ángulo y la hipotenusa Coseno
Coseno, es la razón (división) entre el cateto adyacente al ángulo y la hipotenusa Tangente
tangente, es la razón entre el cateto opuesto al ángulo y el cateto adyacente al mismo. Estas tres (seno, coseno, tangente) son las razones fundamentales que se pueden establecer entre un ángulo agudo y los lados del triángulo rectángulo del cual forman parte. A cada razón fundamental corresponde una razón recíproca, llamadas así por que cada una es la inversa de otra fundamental. Las tres siguientes son las razones recíprocas que se pueden establecer respecto al mismo ángulo: Cosecante
cosecante, es la razón entre la hipotenusa y el cateto opuesto al ángulo, y como es la recíproca del seno de α se puede expresar como
Secante
secante, es la razón entre la hipotenusa y el cateto adyacente al ángulo, y como es la reciproca del coseno de α se puede expresar como
Cotangente
cotangente, es la razón entre el cateto adyacente al ángulo y el cateto puesto al mismo, y como es la recíproca de la tangente de α se puede expresar como
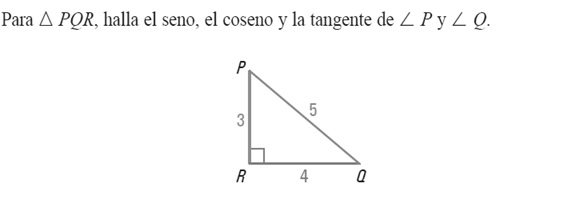
Ejemplo: Hallar las siguientes razones trigonométricas.

Ejemplo 2: Resolver mediante el teorema de Pitágoras.

Ejemplo 3: Seno, Coseno y tangente de un ángulo.


Ejercicios: Conteste correctamente lo que se te pide a continuación.

Graficas de funciones trigonométricas Las gráficas de las funciones trigonométricas poseen propiedades matemáticas muy interesantes como máximo, mínimo, asíntotas verticales, alcance y periodo entre otras. Es necesario estudiar la forma de la gráfica de cada función trigonométrica. Esta forma está asociada a las características particulares de cada función. En la figura de abajo se presentan algunas gráficas de funciones trigonométricas.
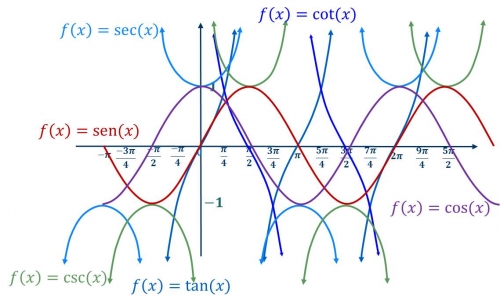
Al establecer relaciones entre dos conjuntos mediante las funciones trigonométricas se establecen relaciones como y=sen(x), y=cos(x), y=tan(x), y=cot(x), y=csc(x) o y=sec(x). La expresión en el paréntesis se denomina argumento de la función (dominio) mientras que yrepresenta el alcance (imágenes). Las gráficas de estas funciones se extienden sobre los ejes coordenados, si es sobre el eje de x, tienen la característica de repetirse por intervalos. Esto significa que cada cierta cantidad de radianes, una parte de la gráfica de la función es la misma (periodo). La extensión sobre el eje de y se conoce como alcance. El modelo de las gráficas de las funciones trigonométricas se obtiene evaluando la función para ángulos que forman una revolución completa.
Gráfica de la Función Seno del ángulo El modelo de la gráfica de la función seno del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas. La función seno del ángulo utiliza la y de los arcos del círculo unitario. El ciclo fundamental de la función seno del ángulo comienza en 0 y termina en2π. En esta figura se observa la relación entre la circunferencia unitaria y la gráfica de la función seno del ángulo x. Además de mostrar el desarrollo de la gráfica de la función seno del ángulo x a partir de la circunferencia unitaria.
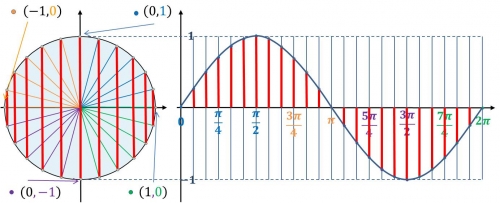
Características: y=sen(x)
|
||||||||||||||||||||