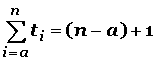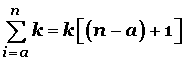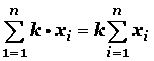3.4.1      Notación de sumatoria y propiedades.

El operando matemático que nos permite representar sumas de muchos sumandos, n o incluso infinitos sumandos está expresado con la letra griega sigma (sigma mayúscula, que corresponde a nuesta S de "suma" ). La notación sigma es de la siguiente manera:

Esto se lee: Sumatorio sobre i, desde m hasta n, de x sub-i.

La variable i es el índice de suma al que se le asigna un valor inicial llamado límite inferior, m. La variable i recorrerá los valores enteros hasta alcanzar el límite superior, n. Necesariamente debe cumplirse que:

 
Si queremos expresar la suma de los cinco primeros números naturales podemos hacerlo de esta forma:

Propiedades

1) Cuando el límite inferior sea un entero mayor que 1, la cantidad de términos  (sumandos) de una sumatoria se obtiene haciendo: límite superior (n) menos límite inferior (a) más la unidad (1):

  2) La sumatoria de una constante (k) es igual al producto (la multiplicación) entre dicha constante (k)  y  la cantidad de sumandos (términos) :

3) La suma del producto de una constante (k) por una variable (x), es igual a k veces la sumatoria de la variable.