1.1.2 Tipos de conjuntos
|
Conjunto unitario Es el conjunto que tiene un solo elemento Ejemplo F= {x| 2x+6=0}

Conjunto infinito Cuando los elementos o miembros no se pueden enumerar o contar, se considera como conjunto infinito.
 Conjunto finito Es el conjunto con limitado número de elementos Ejemplo N= {x | números menores a 9 } E= {x | 0<x<9}
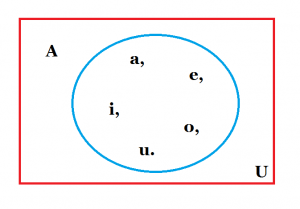
Subconjuntos. Si cada elemento de un conjunto A es también un elemento del conjunto B, entonces se dice que A es un subconjunto de B. también se dice que A está contenida en B o que B contiene a A. este se escriben como: Aᴄ B o BᴐA SI A no es un subconjunto de B, entonces escribiremos. AȼB Ejemplo: las vocales son un subconjunto de las letras del alfabeto

Conjunto universo. El conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universo.
Ʋ= {1, 2, 3, 4,5}
N= {1, 2, 3,4,....} . Usaremos el símbolo Ʋ para denotarlo.
Conjunto vacío. Dado un conjunto Ʋ y una propiedad P puede que no haya elementos en Ʋ que tengan la propiedad P. El conjunto que carece de elementos se llama “conjunto vacío” y se denota por el símbolo Ø. Por ejemplo: A= {Las personas que vuelan} M= {números mayores que 9 y menores que 5}
P= {Ø}
Subconjunto propio. Cundo AᴄB pero A B decimos que “A es un subconjunto propio de B”. Por ejemplo: A= {1,3} B= {1, 2,3} C= {1, 3,2} A es un subconjunto propio de C, mientras que B no es un subconjunto propio de C, ya que B=C Algunos autores manejan la siguiente notación A⊆B para decir que A es un subconjunto de B A ᴄ B para designar que A es subconjunto propio de B
Conjunto potenciaDado un conjunto S, se llama conjunto potencia o conjunto de partes de S (se denota por P(S) o 2S) al conjunto formado por todos los subconjuntos posibles de S. Por ejemplo, si S= {a, b, c} entonces el conjunto potencia de S es P(S) = {{ }, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.
|