3.1    Progresiones aritmética y geométrica.

Ejemplo: Escalera de Jacob:

En el rasca cielos que Jacob posee hay una escalera que va desde el suelo hasta la cima. El primer
escalón mide 8 pulgadas los posteriores miden 9 pulgadas. ¿A que altura del suelo esta el escalón 800?
a1 = 8
a2 = 8 + 1(9) = 17
a3 = 8 + 2(9) = 26
a4 = 8 + 3(9) = 35
...
a800 = 8 + 799(9) = 7199
Por lo tanto el escalón 800 esta a 7199 pulgadas sobre el suelo.

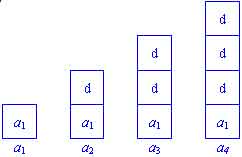
Definición:

Una progresión aritmética es una sucesión infinita de números donde cualquier termino (distinto de primero) se obtiene sumando un numero fijo al anterior. Si se denota a tal sucesión como a1, a2, a3, ... satisface la formula recursiva a_n = a_n-1 + d donde d es un numero fijo llamado diferencia común. 

¿Se puede obtener también una fórmula explícita? Sí. Veamos primero la siguiente figura:
Hay

Hay que observar que las d's deben sumarse con a1 una vez menos que el subíndice de a. Esto significa que: an = a1 + (n - 1)d

Entonces: an = 5 + (n - 1)(4) = 1 + 4n bn = 2 + (n - 1)(.5) = 1.5 + .5n cn = 8 + (n - 1)(-3) = 11 - 3n

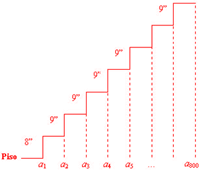
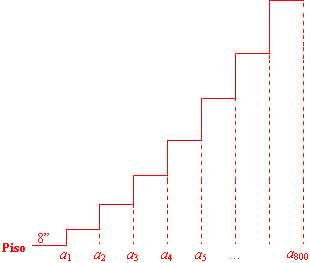
Progresiones Geométricas 

Ejemplo: Escalera de Oro de Jacob.

En sus sueños Jacob vio una escalera de oro con ángeles subiendo y bajando. El primer escalón era de 8
pulgadas, pero después cada escalón tenia una altura de 5/4 pulgadas más que el anterior. ¿A que altura
estará el escalón 800?

a1 = 8

a2 = 8 (5/4)

a3 = 8 (5/4)²

a4 = 8 (5/4)³ 

... a800 = 8 (5/4)⁷⁹⁹

^{Por lo tanto la altura del escalón 800 es de 8 (5/4)799 pulgadas arriba del piso.} 

Definición:

Una progresión geométrica es una sucesión infinita de números donde cualquier término (distinto del primero), se obtiene multiplicando un numero fijo al termino anterior. 

Así una sucesión geométrica a1, a2, a3, ... satisface la formula recursiva

a_n = r a_n-1

donde r es un número fijo llamado razón común.

Además se tiene a2 / a1 = a3 / a2 = a4 / a3 = ... = a_n / a_n-1 = r.

Para obtener la formula explícita correspondiente se tiene que a2 = r(a1) a3 = r(a2) = r(r · a1) = r²(a1) a4 = r(a3) = r(r² · a1) = r³(a1) ...

n-1 ·

a_n = ra1 En este caso el exponente de r es uno menos que el subíndice de a. Esto significa que:

n-1

a_n = a1 · r

Así:

a_n = (3)(2)^n-1 b_n = (12)(1/3)^n-1 c_n = (0.6)(10)^n-1