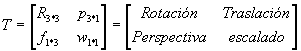3.2.1 Transformación de Matrices Homogéneas

La representación mediante coordenadas homogéneas de la localización de sólidos e n un espacio dimensional se realiza a través de coordenadas de un espacio (n+1)-dimensional. Es decir, un espacio n-dimensional se encuentra representado en coordenadas homogéneas por (n+1) dimensiones, de tal forma que un vector p(x,y,z) vendrá representado por p(wx,wy,z,w), donde w tiene un valor arbitrario y representan un factor de escala.  

A partir de la definición de las coordenadas homogéneas surge inmediatamente el concepto de matriz de transformación homogénea. Se define como matriz de transformación homogénea T a una matriz de dimensión 4*4 que representa la transformación de un vector de coordenadas homogéneas de un sistema de coordenadas a otro.

Así pues, se puede considerar que una matriz homogénea se haya compuesta por cuatro submatrices de distinto tamaño: una submatriz R3*3 que corresponde a una matriz de rotación; una submatriz p3*1 que corresponde al vector de traslación; una submatriz f1*3 que representa una transformación de perspectiva, y una submatriz w1*1 que representa un escalado global. En robótica generalmente solo interesara conocer el valor de R3*3 y de p3*1 , considerándose las componentes f1*3 nulas y la de w1*1 la unidad, aunque mas adelante se estudia su utilidad en otros campos. Al tratarse de una matriz 4*4, los vectores sobre los que se aplique deberán contar con 4 dimensiones, que serán las coordenadas homogéneas del vector tridimensional de que se trate.

Si como sé a mencionado, se considera la transformación de perspectiva nula y el escalado global unitario, la matriz homogénea T resultara de la siguiente forma:

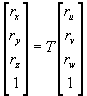
que representa la orientación y posición de un sistema 0’UVW rotado y trasladado con respecto al sistema de referencia 0XYZ. Esta matriz sirve para conocer las coordenadas (rx,ry,rz) del vector r en el sistema 0XYZ a partir de sus coordenadas (ru,rv,rw) en el sistema 0’XYZ:

En resumen, una matriz de transformación homogénea se puede aplicar para:

1. Representar la posición y orientación de un sistema girado y trasladado O’UVW con respecto a un sistema fijo de referencia oxyz, que es lo mismo que representar una rotación y traslación realizada sobre un sistema de referencia.
2. Transformar un vector expresado en coordenadas con respecto a un sistema O’UVW, a su expresión en coordenadas del sistema de referencia OXYZ.
3. Rotar y trasladar un vector con respecto a un sistema de referencia fijo 0XYZ.