Flip-Flops
Los circuitos secuenciales son aquellos en los cuales su salida depende de la entrada presente y pasada. Dentro de estos circuitos se tienen a los Flip-Flops.
Los Flip-Flops son los dispositivos con memoria mas comúnmente utilizados. Sus características principales son:
- Asumen solamente uno de dos posibles estados de salida.
- Tienen un par de salidas que son complemento una de la otra.
- Tienen una o mas entradas que pueden causar que el estado del Flip-Flop cambie.
A continuación se describirán 4 tipos de Flip-Flops.
Flip-Flop S-R (Set-Reset)
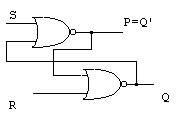
La siguiente figura muestra una forma posible de implementar un Flip-Flop S-R. Utiliza dos compuertas NOR. S y R son las entradas, mientras que Q y Q’ son las salidas (Q es generalmente la salida que se busca manipular).
Como existen varias formas de implementar un Flip-Flop S-R (y en general cualquier tipo de Flip-Flop) se utilizan diagramas de bloque que representen al Flip-Flop. El siguiente diagrama de bloque representa un FF S-R. Nótese que ahora, por convención, Q se encuentra en la parte superior y Q’ en la inferior. 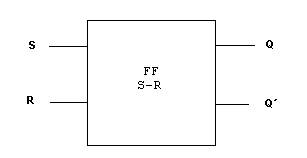
Para describir el funcionamiento de un FF se utilizan las llamadas Tablas de Estado y las Ecuaciones Características. La siguiente tabla muestra la tabla de estado para un FF S-R.
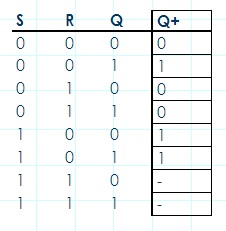 Como encabezado de las columnas tenemos las entradas S y R, y una de las salidas Q. La salida Q es la salida que en un tiempo t se puede detectar en el FF, es decir, es la salida en el tiempo actual. Q+ es la salida en el tiempo Como encabezado de las columnas tenemos las entradas S y R, y una de las salidas Q. La salida Q es la salida que en un tiempo t se puede detectar en el FF, es decir, es la salida en el tiempo actual. Q+ es la salida en el tiempo  , una vez que se ha propagado la señal en el circuito (recuerde que los FF tienen un componente de retroalimentación.) Por lo tanto , una vez que se ha propagado la señal en el circuito (recuerde que los FF tienen un componente de retroalimentación.) Por lo tanto  , es decir, es la salida que tendrá Q en el futuro – una vez que se haya realizado la propagación. , es decir, es la salida que tendrá Q en el futuro – una vez que se haya realizado la propagación.
Si analizamos la tabla de estado, vemos que para si S = 0, R = 0 y Q = 0 ó 1, la salida futura de Q (Q+) será siempre lo que se tenía antes de la propagación. A este estado (S = 0, R = 0) se le conoce por tanto como estado de memoria.
Viendo ahora el caso S = 0, R = 1, se aprecia que siempre Q+ = 0 sin importar el valor de Q antes de la propagación, es decir, se hace un reset de Q. Si por el contrario, se tiene S = 1, R = 0, entonces Q+ = 1 en ambos casos, por tanto se hace un set de Q.
Finalmente, nótese que la combinación S = 1, R = 1 no es valida en el FF S-R. La razón es que dicho estado vuelve inestable al circuito y, como una de las características de todo FF es que el estado es estable, al usar dicha combinación se esta violando este principio de los FF.
Ahora, si se mapea la información de la tabla de estado del FF S-R en un mapa de Karnaugh, se obtiene la siguiente ecuación característica: . Esta ecuación describe también el funcionamiento. Nos dice que Q+ será 1 siempre y cuando se haga un set del FF o el reset no esta activado y la salida tiene un 1 en ese momento.
Flip-Flop T
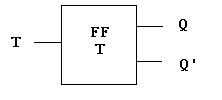
El Flip-flop T cambia de estado en cada pulso de T. El pulso es un ciclo completo de cero a 1. Las siguientes dos figuras muestran el diagrama de bloque y una implementación del FF T mediante un FF S-R y compuertas adicionales.
 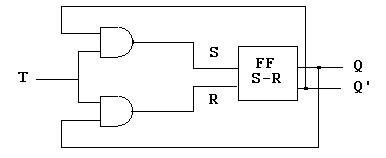
Nótese que en la implementación del FF T, las dos entradas del FF S-R están conectadas a compuertas AND, ambas conectadas a su vez a la entrada T. Además, la entrada Q esta conectada a R y Q’ a S. Esta conexión es así para permitir que el FF S-R cambié de estado cada que se le mande un dato a T. Por ejemplo, si Q = 1 en el tiempo actual, eso significa que Q’ = 0, por lo tanto, al recibir T el valor de 1, se pasaran los valores de R = 1 y S = 0 al FF S-R, realizando un reset de Q.
La siguiente tabla muestra el comportamiento del FF T y del FF S-R en cada pulso de T:
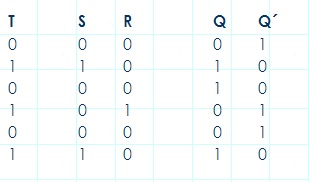 La tabla de estado para el FF T se presenta a continuación. Es muy sencilla: cuando T = 0 el estado de Q no cambia, es decir Q = Q+ (estado de memoria), cuando T = 1, Q es complementada y, por lo tanto, Q+ = Q’. La tabla de estado para el FF T se presenta a continuación. Es muy sencilla: cuando T = 0 el estado de Q no cambia, es decir Q = Q+ (estado de memoria), cuando T = 1, Q es complementada y, por lo tanto, Q+ = Q’.
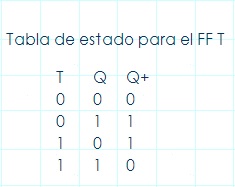
De la tabla de estado anterior, se obtiene la siguiente ecuación característica para el FF T.
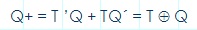
Ahora bien, analicemos un poco más el comportamiento del FF T y tratemos de responder la siguiente pregunta: ¿Qué pasa si T=1 por mucho tiempo?
Los valores de S y R cambiarían constantemente de la siguiente manera:
- S = 0-> 1 -> 0 -> 1
- R= 1-> 0 ->1 -> 0
es decir, el FF empezaría a oscilar y por tanto no mantendría el estado (inestable.) Por lo tanto, la mayoría de los FF utilizan un reloj para determinar en que momento se tomará en cuenta el valor que se encuentre en la entrada del FF. La siguiente figura muestra un FF T con reloj (CK).
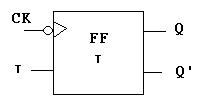
Notese que la entrada marcada como CK tiene un círculo. Este círculo indica que el FF tomará en cuenta la entrada del FF cuando el pulso del reloj sea cero (0). Si es uno (1), la entrada no será tomada en cuenta.
Flip-Flop J-K
El flip-flop J-K es una mezcla entre el flip-flop S-R y el flip-flop T. Esto ocurre de la siguiente manera:
- En J=1, K=1 actúa como Flip-flop T
- De otra forma, actúa como flip-flop S-R
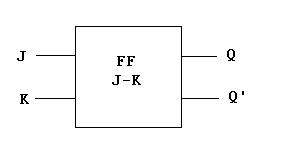
El siguiente diagrama de bloque es el perteneciente el FF J-K:
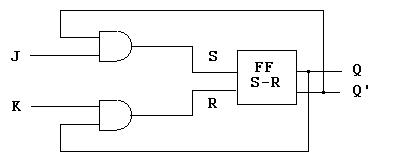
 Una implementación tentativa de un FF J-K a partir de un FF S-R sin reloj es la siguiente: Una implementación tentativa de un FF J-K a partir de un FF S-R sin reloj es la siguiente:
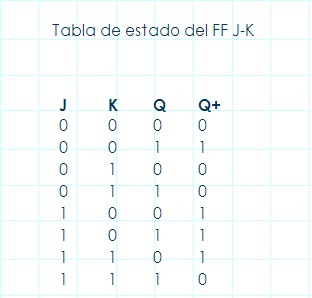
La tabla de estado aparece a continuación. Note que es muy parecida a la del FF S-R solo que ahora los estados de J=1 y K=1 sí son validos.
De la tabla anterior se obtiene la siguiente ecuación característica mediante mapas de Karnaugh:  . Este flip-flop es uno de los más comunes con reloj. El siguiente diagrama lo muestra con entrada para reloj: . Este flip-flop es uno de los más comunes con reloj. El siguiente diagrama lo muestra con entrada para reloj:
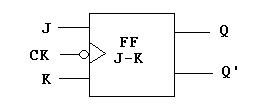 Flip-Flop D (Delay) Flip-Flop D (Delay)
El flip-flop D es uno de los FF más sencillos. Su función es dejar pasar lo que entra por D, a la salida Q, después de un pulso del reloj. Es, junto con el FF J-K, uno de los flip-flops más comunes con reloj. Su tabla de estado se muestra a continuación:
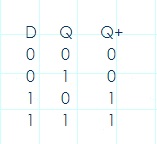
De la tabla se infiere que la ecuación característica para el FF D es: Q+= D. El siguiente diagrama de bloques representa este flip-flop.
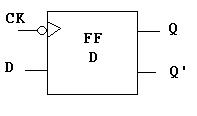
ARRIBA
|