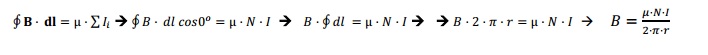3.3 Ley de Ampere
|
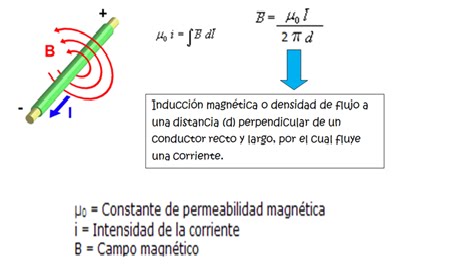
La ley de Biot (1774-1882) y Savart (1791-1841) expresa la relación existente entre la intensidad, I, de una corriente eléctrica rectilínea y estacionaria (de valor constante) y el campo magnético, B, que dicha corriente crea a una cierta distancia, r, de la misma:
Ampére (1775-1836), inspirándose en esta expresión, estableció en 1826 una relación general entre estas dos magnitudes, sea cual sea la forma del conductor por el que circula la corriente de intensidad constante, I:
La ley de Ampere establece que para cualquier trayecto de bucle cerrado, la suma de los elementos de longitud multiplicado por el campo magnético en la dirección de esos elementos de longitud, es igual a la permeabilidad multiplicada por la corriente eléctrica encerrada en ese bucle.
Corriente rectilínea
indefinida.
µ por la suma de intensidades: La corriente rectilínea de intensidad, I, atraviesa la superficie circular delimitada por la circunferencia de radio, r.
Por tanto, igualando (1) a (2) se obtiene:
Solenoide
A la derecha se representa un corte de un pedazo del solenoide. Los puntos representan las corrientes que se dirigen hacia nosotros y las aspas las que se dirigen hacia el interior de la hoja, de modo que cada espira, recorrida por la corriente de intensidad, I, da una media vuelta saliendo por un punto y volviendo a entrar por el aspa correspondiente. Para aplicar la ley de Ampere tomamos un camino cerrado ABCD que es atravesado por varias espiras. Como el campo magnético, B, es constante en el segmento BC y nulo en los otros cuatro segmentos, se obtiene:
NBC/LBC es el número de espiras por unidad de longitud considerada y, por tanto, coincide con N/L (siendo N el número de espiras de todo el solenoide y L su longitud total). Por tanto, bajo las condiciones establecidas, el campo, B, en cualquier punto interior del solenoide es:
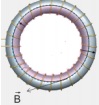
ToroideSi curvamos un solenoide y pegamos sus extremos obtenemos un anillo o toroide. Las líneas de campo magnético, que en el solenoide son segmentos rectos, se transforman en circunferencias concéntricas en el toroide. El campo magnético es tangente en cada punto a dichas circunferencias.
|
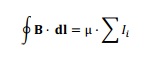
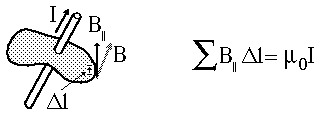
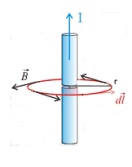 En
la figura adjunta se representa una corriente
rectilínea de intensidad constante, I. Alrededor de
ella se ha dibujado una circunferencia de radio, r,
que es el camino cerrado elegido para hacer circular
al vector B.
En
la figura adjunta se representa una corriente
rectilínea de intensidad constante, I. Alrededor de
ella se ha dibujado una circunferencia de radio, r,
que es el camino cerrado elegido para hacer circular
al vector B. 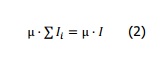
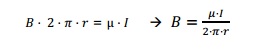
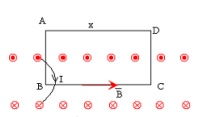 Si
suponemos que el solenoide es muy largo comparado con
el radio de sus espiras, el campo es aproximadamente
uniforme y paralelo al eje en el interior del
solenoide y es nulo fuera del solenoide.
Si
suponemos que el solenoide es muy largo comparado con
el radio de sus espiras, el campo es aproximadamente
uniforme y paralelo al eje en el interior del
solenoide y es nulo fuera del solenoide.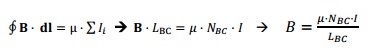
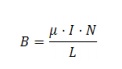
 Elegimos
como camino cerrado una circunferencia de radio r,
cuyo centro está en el eje del toroide, y situada en
su plano meridiano. En este caso, el campo magnético B
está completamente confinado en el interior del
toroide, es tangente a la circunferencia de radio, r,
y tiene el mismo módulo en todos los puntos de dicha
circunferencia. Por tanto, aplicando la ley de Ampere
se obtiene:
Elegimos
como camino cerrado una circunferencia de radio r,
cuyo centro está en el eje del toroide, y situada en
su plano meridiano. En este caso, el campo magnético B
está completamente confinado en el interior del
toroide, es tangente a la circunferencia de radio, r,
y tiene el mismo módulo en todos los puntos de dicha
circunferencia. Por tanto, aplicando la ley de Ampere
se obtiene: