4.1 Modelos de Circuitos Secuenciales

Los circuitos considerados hasta aquí, tienen la característica de que su salida depende solamente de la combinación presente de valores de las entradas, es decir, a una misma combinación de entrada responden siempre con la misma salida. Debido a esto, estos circuitos se denominan combinacionales. 

Los circuitos combinacionales tienen muchas limitantes debido a que no son capaces de reconocer el orden en que se van presentando las combinaciones de entradas con respecto al tiempo, es decir, no pueden reconocer una secuencia de combinaciones, ya que no poseen una manera de almacenar información pasada, es decir no poseen memoria. 

Un circuito cuya salida depende no solo de la combinación de entrada, sino también de la historia de las entradas anteriores se denomina Circuito Secuencial. La historia de las entradas anteriores en un momento dado se encuentra resumida en el estado del circuito, el cual se expresa en un conjunto de variables de estado. 

El circuito secuencial debe ser capaz de mantener su estado durante algún tiempo, para ello se hace necesario el uso de dispositivos de memoria. Los dispositivos de memoria utilizados en circuitos secuenciales pueden ser tan sencillos como un simple retardador (inclusive, se puede usar el retardo natural asociado a las compuertas lógicas) o tan complejos como un circuito completo de memoria denominado multivibrador biestable o Flip Flop.

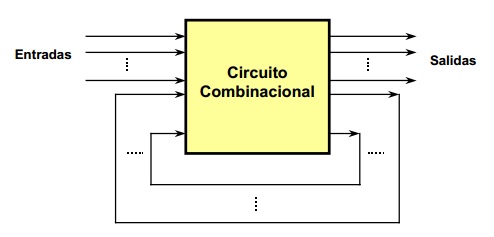
Circuito secuencial asíncrono

En un circuito secuencial asíncrono, los cambios de estado ocurren al ritmo natural marcado por los retardos asociados a las compuertas lógicas utilizadas en su implementación, es decir, estos circuitos no usan elementos especiales de memoria, pues se sirven de los retardos propios (tiempos de propagación) de las compuertas lógicas usados en ellos. Esta manera de operar puede ocasionar algunos problemas de funcionamiento, ya que estos retardos naturales no están bajo el control del diseñador y además no son idénticos en cada compuerta lógica.

Circuito secuencial síncrono

Los circuitos secuenciales síncronos, sólo permiten un cambio de estado en los instantes marcados por una señal de sincronismo de tipo oscilatorio denominada reloj. Con ésto se pueden evitar los problemas que tienen los circuitos asíncronos originados por cambios de estado no uniformes en todo el circuito.

Un circuito secuencial puede entenderse simplemente como un circuito combinacional en el cual las salidas dependen tanto de las entradas como de las salidas en instantes anteriores, esto implica una retroalimentación de las salidas como se muestra en diagrama de la siguiente figura:                          

Multivibradores Biestables (Flip Flops).

Los circuitos secuenciales básicos que funcionan también como unidades de memoria elementales se denominan multivibradores biestables (por tener dos estados estables –alto y bajo-), tambi´pen conocidos como Flip Flops. 

Al definir cada una de las herramientas mencionadas en la lista anterior consideraremos un circuito lógico 
secuencial asíncrono fundamental llamado Flip Flop Set Reset (FF-SR) el cual se describe a continuación con ayuda de las herramientas mencionadas.

El Flip Flop Set Reset FF-SR

El FF-SR es un dispositivo con dos entradas (Set y Reset) y una variable de estado o salida (Q) capaz de “guardar” un bit de información y funciona como sigue: 

• Si su entrada Set se activa su estado Q se pone en Alto 
• Si su entrada Reset se activa su estado Q se pone en Bajo 
• Si no se activa ni Set ni Reset su estado no cambia 
• Por supuesto, no se permite activar Set y Reset simultáneamente.

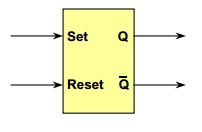
Diagrama de Bloques

Aunque el FF-SR posee dos entradas (S y R) y sólo una salida (Q), es común la implementación que provee demás de Q su versión complementada Q, como se muestra en la figura siguiente:                                                  

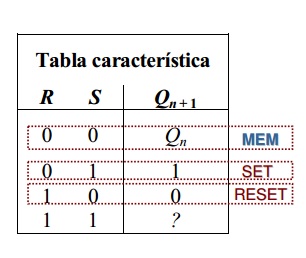
Tabla de Funcionamiento

Los fabricantes de los circuitos integrados usan una tabla de funcionamiento para describir la operación de un circuito de una manera compacta, dicha tabla de funcionamiento no es otra cosa que una tabla de verdad como la usada para circuitos combinacionales, en la cual se ha introducido la información del tiempo que en el caso de circuitos secuenciales se vuelve esencial. Enseguida se ilustrará el uso de esta tabla para describir de manera compacta el funcionamiento del FF-SR.                                                   

Diseño del Flip Flop Set Reset. 

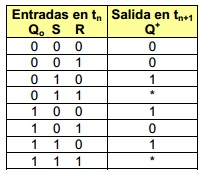
Como ejemplo introductorio, consideraremos el problema de diseñar el Flip Flop-SR. En este caso la salida Q+ depende del estado anterior Qo y de las entradas S y R, es decir:

                                                           

Es decir, el diseño lo plantearemos como si se tratara de un circuito combinacional, pero considerando Qo como si fuera una entrada más. Esta función la podemos plantear por medio de la siguiente tabla de verdad, obtenida de la tabla de estado descrita anteriormente:                                           

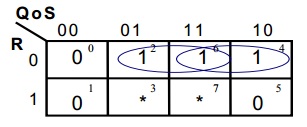
El Mapa de Karnaugh correspondiente es el siguiente:                                         

De donde podemos obtener la expresión siguiente. (Aunque no es un procedimiento común, la experiencia a demostrado que se puede obtener una implementación más sencilla despreciando las condiciones sin cuidado), entonces:                                                    

Para implementar con sólo compuertas NOR negamos dos veces la expresión para obtener:                                             

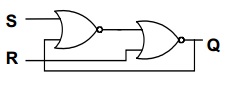
Con lo cual podemos implementar el FF-SR con sólo dos compuertas NOR, como sigue:                                                       

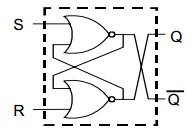
Esta implementación además tiene la ventaja de que también produce la función negada Q a la salida de la primera compuerta NOR, de manera que una mejor manera de dibujar este circuito es como se muestra en la siguiente figura:                                               

ARRIBA