2.8 Circuitos RC (Resistencia en Capasitore)
|
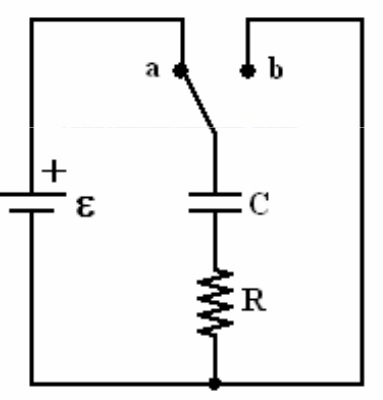
Los circuitos RC son circuitos que están compuestos por una resistencia y un condensador. Se caracteriza por que la corriente puede variar con el tiempo. Cuando el tiempo es igual a cero, el condensador está descargado, en el momento que empieza a correr el tiempo, el condensador comienza a cargarse ya que hay una corriente en el circuito. Debido al espacio entre las placas del condensador, en el circuito no circula corriente, es por eso que se utiliza una resistencia. Cuando el condensador se carga completamente, la corriente en el circuito es igual a cero. La segunda regla de Kirchoff dice: V = (IR) – (q/C) Donde q/C es la diferencia de potencial en el condensador. En un tiempo igual a cero, la corriente será: I = V/R cuando el condensador no se ha cargado. Cuando el condensador se ha cargado completamente, la corriente es cero y la carga será igual a: Q = CV CARGA DE UN CONDENSADOR Ya se conoce que las variables dependiendo del tiempo serán I y q. Y la corriente I se sustituye por dq/dt (variación de la carga dependiendo de la variación del tiempo): (dq/dt)R = V – (q/C) dq/dt = V/R – (q/(RC))Esta es una ecuación Diferencial. Se pueden dq/dt = (VC – q)/(RC) Separar variable dq/(q – VC) = - dt/(RC) Al integrar se tiene ln [ - (q – VC)/VC)] = -t/(RC Despejando q q dt = C V [(1 – e-t/RC )] = q (1- e-t/RC ) El voltaje será Vc (t) = V e1/rc DESCARGA DE UN CONDENSADORDebido a que la diferencia de potencial en el condensador es IR = q/C, la razón de cambio de carga en el condensador determinará la corriente en el circuito, por lo tanto, la ecuación que resulte de la relación entre el cambio de la cantidad de carga dependiendo del cambio en el tiempo y la corriente en el circuito, estará dada remplazando I = dq/dt en la ecuación de diferencia de potencial en el condensador: q = Q e-t/RC Donde Q es la carga máxima La corriente en función del tiempo entonces, resultará al derivar esta ecuación respecto al tiempo: I = Q/(RC) e-t/RC Se puede concluir entonces, que la corriente y la carga decaen de forma exponencial. Se llama circuito RC a la combinación en serie de un capacitor y un resistor. Dicho circuito puede representar cualquier conexión de resistores y capacitores cuyo equivalente sea un solo resistor en serie con un solo capacitor. En la figura se muestra un circuito RC conectado a una fuente de voltaje continuo. El interruptor tiene como objetivo cargar y descargar al capacitor.
El proceso inicia cuando el interruptor se conmuta a la posición “a” en el tiempo t=0 [s] y se considera que el capacitor se encuentra descargado descargado.. Aplicando Aplicando ley de kirchhoff a la malla. |