Una herramienta muy útil para la simplificación de funciones en forma estándar son los mapas de Karnaugh.[4]

En ellos, se coloca un 1 en el recuadro cuyos valores de las variables correspondan a los valores de nuestros términos.

En la expresión en forma estándar:

F=AB'C'D' + ABC'D' + A'BCD' + A'BCD + ABCD' + ABCD

su mapa de Karnaugh quedaría así:

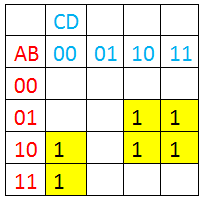
Cuando quedan los '1' juntos, la expresión se puede simplificar.

Siempre que la espresión sea de 4 variables, se puede deducir que:

Si queda un 1 sólo, el término será de cuatro variables.

Si quedan dos 1, el término será de tres variables.

Si quedan cuatro 1, el término será de dos variables.

Si quedan ocho 1, el término será de una variable.

Si quedan dieciséis 1, el término será una tautología.

Al quedar dos juntos, se sabe que quedará un término de tres variables. Cuando A=1:B=1:C=0:D=0 y A=1:B=0:C=0:D=0, se deduce que el valor de B no importa. Por ello el término queda <AC'D'>.   

Cuando hay cuatro '1' junto, el término será de dos variables. Haciendo el mismo análisis se llega a la expresión <BC>.

Por lo tanto, la expresión resultante es:

F=AC'D' + BC