4.1  Atributos y Gramáticas con Atributos

Informalmente, se llamará atributos de un símbolo de la gramática a toda información añadida en el árbol de derivación por el analizador semántico, asociada a los símbolos de los nodos anotados. Un   componente importante de las gramáticas de atributos es el algoritmo de cálculo de los valores.

  • Ejemplos de atributos:
    • Tipo de una variable
    • Valor de una expresión
    • Ubicación en memoria de una variable
    • Código objeto de un procedimiento
    • Número de dígitos significativos en un número 

Una gramática de atributos es una gramática independiente del contexto en la cual a sus símbolos terminales y no terminales se les dota de unos atributos y a sus producciones de unas funciones de evaluación que hacen que dichos atributos se propaguen a través de la gramática. Su fin es conocer un determinado valor de un atributo en cualquier parte del árbol de derivación y tomar la decisión oportuna.

Un atributo es una propiedad asociada a una estructura sintáctica. Si una estructura sintáctica representada por el símbolo gramatical X tiene asociado un atributo a lo representaremos por X.a (Nombre  símbolo.Nombre atributo)

• Ejemplo:

numero -> numero digito | digito

a)      numero-> digito

numero.valor = digito.valor

b)      numero -> numero digito numero1.valor = numero2.valor * 10 + digito.valor

Las funciones semánticas relacionan los valores de los atributos definidos sobre la gramática atribuida y van asociadas a producciones de la gramática atribuida.

 

Ejemplo: Sea el lenguaje L={an |n>=0} generado por la siguiente gramática:

 

 G={ ∑={a, $}, N={S, A}, S, P) P: S→A$ A→aA A→a

 

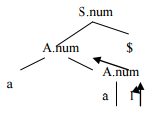
 Se quiere atribuir para que contabilice y escriba el número de aes que tiene una palabra generada.

S→A$ {writeln (A.num)}

A→aA {A1.num=1+A2.num}

A→a {A.num=1}

 		 Figura 4.10 

Definición formal

Una gramática de atributos está formada por una tripleta GA={GIC, A, F}

G – gramática independiente del contexto

 A – atributos asociados a los símbolos terminales y no terminales

F – función de evaluación, función asociada a producción que determina como obtener unos atributos en función de otros dentro de la misma producción

 

A→X1 X2 X3 …Xn ; A∈N y Xi∈(Σ|N)

 A.a=f (X1.a,X2.b,…Xm.z)

 

a es un atributo asociado al símbolo no terminal A y obtiene su valor en función de los atributos: a asociado a X1, b asociado a X2 ,…y z asociado a Xm ( es un atributo obtenido en función de la parte derecha de la producción)

 

X1.a=f (A.a,X2.b)

 

 a es un atributo asociado al símbolo X1 y obtiene su valor en función de los atributos: a asociado a A, b asociado a X2 ( es un atributo obtenido en función de elementos de la parte derecha e izquierda de la producción)

 

 A.a=f (y1.b, B.a) , X1.a=f (y1.b, B.a)     Atributos incorrectos no se obtienen dentro de la producción   

Tipos de atributos:

  • Sintetizados son atributos que se propagan desde las hojas a la raiz ‘

A→X1 X2 X3 …Xn ; A∈N y Xi∈(Σ|N)

 A.a=f(X1.a,X2.b,…Xm.z) a es un atributo sintetizado obtienen sus valores de los atributos de un nivel inferior en la generación del árbol, es decir de la parte derecha de la producción
Figura 4.11

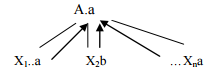S→A$ {writeln (A.num)}

A→aA {A1.num=1+A2.num}

 A→a {A.num=1}
  • Heredados  son atributos que se propagan desde la raiz a las hojas o dentro de un mismo nivel A→X1 X2 X3 …Xn ; A∈N y Xi∈(Σ|N)

 X1.a=f(A.a,X2.b,…) a es un atributo heredado obtenido en función de los atributos a y b obtiene sus valores de los atributos del mismo nivel o superior en la generación del árbol, es decir se calculan descendentemente
Figura 4.12

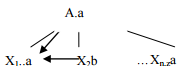S→A$ {A.num=0}

 A→aA {A2.num=1+A1.num}

A→a {writeln (A.num+1}
  • Intrínsecos Son atributos relativos a símbolos terminales, por lo tanto valores correspondes a las hojas (valores finales). Son valores fijos obtenidos de antemano cuyo valor se obtiene de partida. En el ejemplo anterior de contabilizar aes, el valor intrínseco de cada a es 1.
Figura 4.13

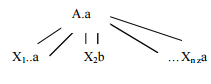S→A$ {writeln (A.num)}

A→aA {A1.num=1+A2.num}

A→a {A.num=1}

Poder de significación de las gramáticas de atributos

La gramáticas de atributos tienen un mayor poder de significación que una gramática independiente del contexto. Puede reconocer lenguajes de tipo superior, es decir de tipo 1 o tipo 0 .

 Sea el lenguaje L={ an bn cn| n>=0} es un lenguaje de tipo 1, solo puede ser generado por una gramática de tipo 1 o 0 .

Se puede construir una gramática de atributos GA=( GIC, A, F) que genere dicho lenguaje:

Sea la gramática: S→AB A→aAb |ε B→cB |ε que genera el lenguaje L={anbncm| n>=0,m>=0} Podemos atribuirla para que genere el lenguaje L={anbncn| n>=0}

 Atributos, necesarios para contabilizar las aes, bes y ces: num_ab atributo sintetizado asociado a A y num_c atributo sintetizado asociado a B Funciones asociadas a las producciones necesarias para la propagación de los atributos:

 

 S→AB {IF A.num_ab<>B.num_c Then error semántico}

A→aAb {A1.num_ab=A2.num_ab+1}

|ε {A1.num_ab=0}

B→cB {B1..num_c=B2.num_c+1}

|ε {B.num_c=0}