2.6.2. Autómatas Finitos Deterministas
|
Un autómata finito determinista (abreviado AFD) es un caso especial de un autómata finito no determinista en el cual.
Un autómata finito tiene a lo sumo una transición desde cada estado con cualquier entrada. Si se esta usando una tabla de transiciones para representar la función de transición de un AFD, entonces cada entrada en la tabla de transiciones es solo un solo estado. Como consecuencia, es muy fácil determinar si un autómata finito determinista acepta o no una cadena de entrada, puesto que hay a lo sumo un camino desde el estado de inicio etiquetado con esa cadena. El siguiente algoritmo muestra como simular el comportamiento de un AFD con una cadena de entrada.
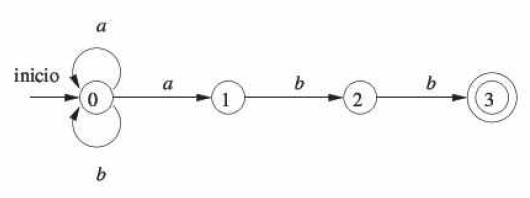
S: =S0; C: =sigtecar; While c ≠ eof do S: = mueve (s,c); C: =sigtecar; End: If s esta en F then Return “si” Else return “no”; Ejemplo. En la siguiente figura se ve al grafo de transiciones de un autómata finito determinista aceptar el mismo lenguaje (a | b)*abb aceptado por el AFN de la figura |
 |
|
Figura 1. Grafo de transiciones de un autómata finito determinista |
|
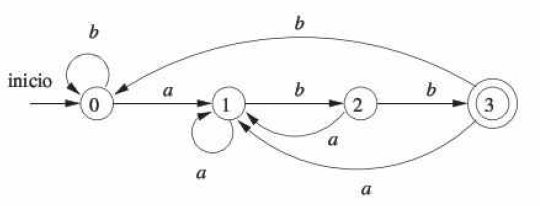
Con este AFD y la cadena de entrada ababb. el algoritmo sigue la secuencia de estados 0, 1, 2, 1, 2, 3 y devuelve "sí". |
 |