3.2 Gramaticas Independientes del Contexto

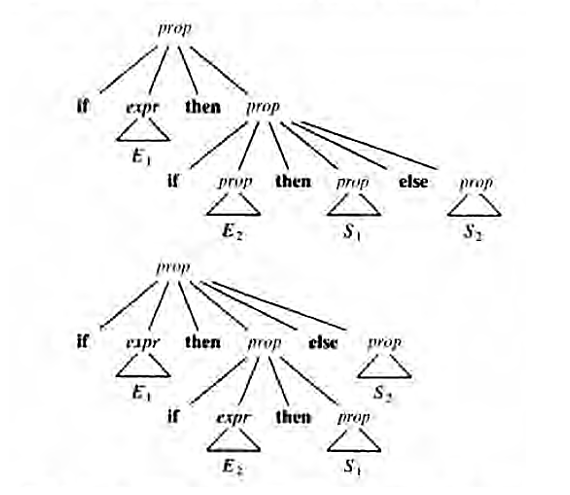
Muchas construcciones de los lenguajes de programación tienen una estructura inherentemente recursiva que se puede definir mediante gramáticas independientes del contexto. Por ejemplo, se puede tener una proposición condicional definida por una regla como:

Si S₁ y S₂ son proposiciones y E es una expresión, entonces

"If E then S₁ else S₂” es una proposición.  (1)

No se puede especificar esta forma de proposición condicional usando la notación de las expresiones regulares; las expresiones regulares pueden especificar la estructura lexicográfica de los componentes léxicos. Por otro lado, utilizando la variable sintáctica prop para denotar la clase de las proposiciones y expr para la clase de las expresiones, ya se puede expresar (1) usando la producción gramatical

prop -> if expr then prop else prop (2)

En esta sección se revisa la definición de una gramática independiente del contexto y se introduce terminología para el análisis sintáctico. Una gramática independiente del contexto (gramática, por brevedad) consta de terminales, no terminales, un símbolo inicial y producciones.

1. Los terminales son los si m bolos básicos con que se forman las cadenas. "Componente léxico" es un sinónimo de "terminal" cuando se trata de gramáticas para lenguajes de programación. En (2), cada una de las palabras clave if, then y else es un terminal.
2. Los no terminales son variables sintácticas que denotan conjuntos de cadenas. En (2), prop y expr son no terminales. Los no terminales definen ·conjuntos de cadenas que ayudan a definir el lenguaje generado por la gramática. También imponen una estructura jerárquica sobre el lenguaje que es útil tanto para el análisis sintáctico como para la traducción.
3. En una gramática, un no terminal es considerado como el símbolo inicial, y el conjunto de cadenas que representa es el lenguaje definido por la gramática.
4. Las producciones de una gramática especifican cómo se pueden combinar los terminales y los no terminales para formar cadenas. Cada producción consta de un no terminal, seguido por una flecha (a veces se usa el simbolo :: =, en lugar de la flecha), seguida por una cadena de no terminales y terminales.

Ejemplo La gramática con las siguientes producciones define expresiones aritméticas simples.

Expr-> expr op expr

expr -> ( expr )

expr -> -expr

expr -> id

op -> +

OP -> -

op ->*

op ->/

op -> |

En esta gramática, los símbolos terminales son:

id  + -  * /  | ()

Los símbolos no terminales son expr y op, y expr es el símbolo inicial.

Convenciones de notación

Para evitar tener que establecer siempre que "estos son los terminales'', "estos son los no terminales'', etcétera, a partir de ahora se emplearán las siguientes convenciones de notación con respecto a las gramáticas.

1. Estos símbolos son terminales:
   1. Las primeras letras minúsculas del alfabeto, como a, b, c.
   2.  Los símbolos de operador como +, - , etcétera.
   3. Los símbolos de puntuación como paréntesis, coma, etcétera.
   4. Los dígitos 0, 1, .... , 9.
   5. Cadenas en negritas, como id o if
   6. Estos símbolos son no terminales:
      1. Las primeras letras mayúsculas del alfabeto, como A, B, C.
      2.  La letra S. que cuando aparece suele ser el símbolo inicial.
      3.  Los nombres en cursivas minúsculas, como expr o prop.
      4. Las últimas letras mayúsculas del alfabeto, como X, Y, Z. representan símbolos gramaticales, es decir, terminales o no terminales.
      5. Las últimas letras minúsculas del alfabeto, principalmente u, v, . .. . z, representan cadenas de terminales.
      6. Las letras griegas minúsculas α, β, γ, por ejemplo, representan cadenas de símbolos gramaticales. Por tanto, una producción genérica podría escribirse A -> α, indicando que hay un solo no terminal A a la izquierda de la flecha (el lado izquierdo de la producción) y una cadena de símbolos gramaticales α a la derecha de la flecha (el lado derecho de la producción).
      7. Si A -> α₁ , A-> α₂, ...., A-- α_n· son todas producciones con A a la izquierda (se les llama producciones de A), se puede  escribir A-> α₁, |α₂|,…,|α_n, α_n, α_n,… α_n| se denominan alternativas de A.
      8. A menos que se diga otra cosa, el lado izquierdo de la primera producción es el símbolo inicial.

Derivaciones

Hay varias formas de considerar el proceso mediante el cual una gramática define un lenguaje, esta visión derivativa da una descripción precisa de la construcción descendente de un árbol de análisis sintáctico. La idea central es que se considera una producción como una regla de reescritura, donde el no terminal de la izquierda es sustituido por la cadena del lado derecho de la producción.

Por ejemplo, considérese la siguiente gramática para expresiones aritméticas, donde el no terminal E representa una expresión.

E-> E + E |E*E| (E)| - E|id   (1)

La producción E -> - E significa que una expresión precedida por un signo menos es también una expresión. Esta producción se puede usar para generar expresiones más complejas a partir de expresiones más simples permitiendo sustituir cualquier presencia de E por - E. En el caso más simple, se puede sustituir una sola E por - E. Se puede describir esta acción escribiendo

E => - E

que se lee ''E deriva – E”. La producción E-> (E) establece que también se podría sustituir una presencia de una E en cualquier cadena de símbolos gramaticales por (E); por ejemplo, E* E=> (E)*E o *E=> E*(E).

Se puede tomar una sola E y aplicar repetidamente producciones en cualquier orden para obtener una secuencia de sustituciones. Por ejemplo,

E=> - E => - (E) => - (id)

A dicha secuencia de sustituciones se le llama derivación de - (Id) a partir de E. Esta derivación proporciona una prueba de que un caso determinado de una expresión es la cadena -(id).

De forma más abstracta, se dice que αAβ => αγβ si A => γ es una producción y α y β son cadenas arbitrarias de símbolos gramaticales. Si α₁ => α₂ => ... => α_n, se dice que α₁ deriaa a α_n. El símbolo => significa "deriva en un paso". A menudo se desea decir "deriva en cero o más pasos". Para este propósito se puede usar el símbolo *=>. Así:

1. α *=> α para cualquier cadena α, γ
2. Si α *=> β y β => y, entonces α*=>γ.

Del mismo modo se puede usar +=> para expresar "deriva en uno o más pasos".

Dada una gramática G con símbolo inicial S, se puede utilizar la relación +=> para definir L(G), el lenguaje generado por G. Las cadenas de L(G) pueden contener sólo símbolos terminales de G. Se dice que una cadena de terminales w está en L(G) si, y sólo si, S+=>w. A la cadena w se le llama frase de G. De un lenguaje que pueda ser generado por una gramática se dice que es un lenguaje independiente del contexto. Si dos gramáticas generan el mismo lenguaje, se dice que son equivalentes.

Si S*=α, donde α puede contener no terminales, entonces se dice que α es una forma de frase de G. Una frase es una forma de frase sin no terminales.

Ejemplo  La cadena -(id + id) es una frase de la gramática (1), porque existe la derivación:

E=> - E=> - (E) => - (E+E) => - (id + E) => - (id + id)             (2)

Las cadenas E, -E, - (E), ... , -(id + íd) que aparecen en esta derivación son todas formas de frases de esta gramática. Se escribe E*=>- (id + id) para indicar que - (id + id) se puede derivar de E.

Se puede demostrar por inducción sobre la longitud de una derivación que toda frase del lenguaje de la gramática (1) es una expresión aritmética que comprende a los operadores binarios + y *, al operador unario -, paréntesis y al operando id. De manera similar, se puede demostrar por inducción sobre la longitud de una expresión aritmética que todas estas expresiones pueden ser generadas por esta gramática. Así, la gramática (1) genera precisamente el conjunto de todas las expresiones aritméticas que comprenden a los binarios + y *, al – unario, a los paréntesis y al operando id.

En cada paso de una derivación hay que hacer dos elecciones. Es necesario escoger qué no terminal se debe sustituir y, una vez hecha esta elección, qué alternativa usar para este no terminal. Por ejemplo, la derivación (2) del ejemplo  podría continuar desde -(E+ E) como sigue

                    - (E+E) => - (E+ id) => - (id + id)                      (3)

Se sustituye cada no terminal de (3) por el mismo lado derecho que en el ejemplo, pero el orden de sustitución es diferente. Para comprender cómo trabajan algunos analizadores sintácticos, hay que considerar derivaciones donde tan sólo el no terminal de más a la izquierda de cualquier forma de frase se sustituya a cada paso. Dichas derivaciones se denominan por la izquierda. Si α=>β mediante un paso en el que se sustituye el no terminal más a la izquierda de α, se escribe α=>β· Puesto que la derivación (2) es por la izquierda, se puede escribir así:

E=> - E=> - (E) => - (E+E) => - (id+E) => - (id + id)

Usando las convenciones de notación, todo paso por la izquierda se puede escribir ωAγ =>ωδγ, donde ω consta sólo de terminales, A-> δ es la producción aplicada y γ es una cadena de símbolos gramaticales. Para subrayar el hecho de que α deriva a β por medio de una derivación por la izquierda, se escribe α*=>β. Si  S*=>α entonces se dice que α es una forma de frase izquierda de la gramática en cuestión. Análogas definiciones se aplican a las derivaciones derechas, donde el no terminal más a la derecha se sustituye en cada paso. Las derivaciones derechas a menudo se denominan derivacion.es canónicas.

Arboles de análisis  sintáctico y derivaciones

Un árbol de análisis sintáctico se puede considerar como una representación gráfica de una derivación que no muestra la elección relativa al orden de sustitución. Las hojas del árbol de análisis sintáctico se etiquetan con terminales o no terminales y, leídas de izquierda a derecha, constituyen una forma de frase, llamada el producto o frontera del árbol. Por ejemplo, en la figura  se muestra el árbol de análisis sintáctico para -(id+ id) indicado por la derivación (2).

Para ver la relación entre las derivaciones y los árboles de análisis sintáctico, considere cualquier derivación α₁ =>α₂=>• • • => α_n, en donde αi es un sólo no terminal A. Para cada forma de frase α_i en la derivación, podemos construir un árbol de análisis sin táctico cuyo producto sea α_i. El proceso es una inducción sobre i.

BASE: El árbol para α_i = A es un solo nodo, etiquetado como A.

INDUCCIÓN: Suponga que ya hemos construido un árbol de análisis sintáctico con el producto α_i-1 = X₁X₂… X_k (tenga en cuenta que, de acuerdo a nuestras convenciones de notación, cada símbolo gramatical X_i es un no terminal o un terminal).

 Suponga que α_i se deriva de α_i-1 al sustituir X_j, un no terminal, por β = Y_i Y₂… Y_m. Es decir, en el i-ésimo paso de la derivación, la producción Xj - > β   se aplica α_i-1 para derivar α_i=X₁X₂…X_j-1βX_j+1…X_k

Para modelar este paso de la derivación, buscamos la j-ésima hoja, partiendo de la izquierda en el árbol de análisis sintáctico actual. Esta hoja se etiqueta como X_j. A esta hoja le damos m hijos, etiquetados Y₁ Y₂, . .. ,Y_m, partiendo de la izquierda. Como caso especial, si m = 0 entonces β = Є, y proporcionamos a la j-ésima hoja un hijo etiquetado como Є.

Ambigüedad

Se dice que una gramática que produce más de un árbol de análisis sintáctico para alguna frase es ambigua, o, dicho de otro modo, una gramática ambigua es la que produce más de una derivación por la izquierda o por la derecha para la misma frase. Para algunos tipos de analizadores sintácticos es preferible que la gramática no sea ambigua, pues si lo fuera, no se podría determinar de manera exclusiva qué árbol de; análisis sintáctico seleccionar para una frase. Para algunas aplicaciones se considerarán también los métodos mediante los cuales se puedan utilizar ciertas gramáticas ambiguas, junto con reglas para eliminar ambigüedades que desechan árboles de análisis sintáctico indeseables, dejando sólo un árbol para cada frase.