3.3 Escritura de una Gramática
|
Las gramáticas son capaces de describir la mayoría, pero no todas, de las sintaxis de los lenguajes de programación. Un analizador léxico efectúa una cantidad limitada de análisis sintáctico conforme produce la secuencia de componentes léxicos a partir de los caracteres de entrada. Ciertas limitaciones de la entrada, como el requisito de que los identificadores se declaren antes de ser utilizados, no pueden describirse mediante una gramática independiente del contexto. Por tanto, las secuencias de componentes léxicos aceptadas por un analizador sintáctico forman un superconjunto de un lenguaje de programación; las fases posteriores deben analizar la salida del analizador sintáctico para garantizar la obediencia a reglas que el analizador sintáctico no comprueba. Expresiones regulares, o gramáticas independientes del contexto Toda construcción que se pueda describir mediante una expresión regular también se puede describir por medio de una gramática. Por ejemplo, la expresión regular (a|b)*abb y la gramática A0 -> αA0 | bA0 | αA1 A1 -> bA2 A2-> bA3 A3-> Є Describen el mismo lenguaje, el conjunto de cadenas de caracteres a y b que terminan en abb. Se puede convertir de manera mecánica un autómata finito no determinista (AFN) en una gramática que genere el mismo lenguaje reconocido por el AFN. Puesto que todo conjunto regular es un lenguaje independiente del contexto, es razonable preguntar: ¿Por qué utilizar expresiones regulares para definir la sintaxis lexicográfica de un lenguaje? Existen varias razones.
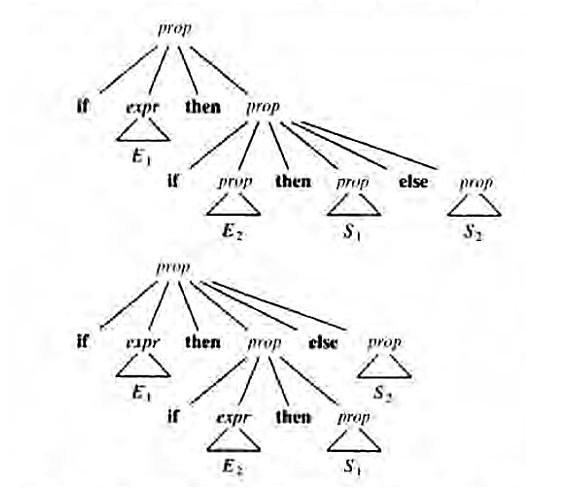
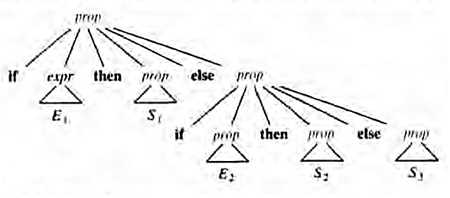
No existen normas fijas en cuanto a qué poner en las reglas lexicográficas, en vez de las reglas sintácticas. Las expresiones regulares son muy útiles para describir la estructura de las construcciones léxicas, como identificadores, constantes, palabras clave, etcétera. Las gramáticas, por otra parte, son muy útiles para describir estructuras anidadas, como paréntesis equilibrados, concordancia de las palabras clave begin y end, los correspondientes if-tben-else, etcétera. Como ya se ha señalado, estas estructuras anidadas no se pueden describir con expresiones regulares. Comprobación del lenguaje generado por una gramática Aunque los diseñadores de compiladores rara vez lo hacen para una gramática completa de un lenguaje de programación, es importante ser capaz de razonar que un conjunto dado de producciones genera un lenguaje determinado. Las construcciones problemáticas se pueden estudiar escribiendo una gramática abstracta concisa y estudiando el lenguaje que genera. Más adelante se construirá una de estas gramáticas para los condicionales. Una prueba de que una gramática G genera un lenguaje L tiene dos partes: se debe demostrar que toda cadena generada por G está en L, y lo opuesto, que toda cadena de L puede de hecho ser generada por G. Supresión de la ambigüedad A veces, una gramática ambigua se puede reescribir para eliminar la ambigüedad. Como ejemplo, se eliminará la ambigüedad de la siguiente gramática con "else ambiguo” prop ->if expr then prop | if expr then prop else prop (1) | otra Aquí, otra representa cualquier otra proposición. De acuerdo con esta gramática la proposición condicional compuesta if E1 then S1 else if E2 then S2 else S3 tiene el árbol de análisis sintáctico que se muestra en la figura La gramática (1) es ambigua, puesto que la cadena if E1 then if E2 then S1 else S2 (2) |
 |
| Figura 4.3 Árbol de análisis sintáctico |
|
Tiene los dos árboles de análisis sintáctico que se muestran en la siguiente figura dos árboles de análisis sintáctico para una frase ambigua. |
|
|
|
Figura 4.4 Árboles de análisis sintáctico para una frase ambigua |
|
En todos los lenguajes de programación con proposiciones condicionales de esta forma, se prefiere el primer árbol de análisis sintáctico. La regla general es, "emparejar cada else con el then sin emparejar anterior más cercano". Esta regla para eliminar ambigüedades se puede incorporar directamente a la gramática. Por ejemplo, se puede reescribir la gramática (1) como la siguiente gramática no ambigua. La idea es que una proposición que aparezca entre un then y un else debe estar "emparejada"; es decir, no debe terminar con un then sin emparejar seguido de cualquier proposición, porque entonces el else estaría obligado a concordar con este then no emparejado. Una proposición emparejada es o una proposición if-then-else que no contenga proposiciones sin emparejar o cualquier otra clase de proposición no condicional. Así, se puede utilizar la gramática prop -> prop_emparejada | pro_no_emparejada prop_emparejada -> if expr then prop_emparejada else prop_emparejada |otra prop_no_emparejada -> if expr then prop |if expr then prop_emparejada else prop_no_emparejada Esta gramática genera el mismo conjunto de cadenas que (1), pero permite sólo un análisis sintáctico para la cadena (2), es decir, el que asocia cada else con el then sin emparejar anterior más cercano.
Eliminación de la recursión por la izquierda Una gramática es recursiva por la izquierda si tiene un no terminal A tal que existe una derivación A+=>Aα para alguna cadena α. Los métodos de análisis sintáctico descendente no pueden manejar gramáticas recursivas por la izquierda, así que se necesita una transformación que elimine la recursión por la izquierda. Con la forma A->Aα el par de producciones recursivas por la izquierda A ->Aα|β podían sustituirse por las producciones no recursivas por la izquierda A-> βA' A'-> αA' | Є sin modificar el conjunto de cadenas derivables de A. Esta regla ya es suficiente en muchas gramáticas. Ejemplo. Considérese la siguiente gramática para expresiones aritméticas. E->E + T | T T->T *F | F (1) F-> (E) | id Eliminando la recursión directa por la izquierda (producciones de la forma A ->Aα) a las producciones de E y después a las de T, se obtiene E->TE E-> TE | Є T->FT (2) T-> * FT | Є F-> (E) | id Independientemente de cuántas producciones de A existan, se puede eliminar de ellas la recursión directa por la izquierda mediante la siguiente técnica. Primero se agrupan las producciones de A en la forma A -> Aα1 |Aα2| ... | Aαn| β1| β2| ... | βn donde ninguna β1 comienza con una A. Después se sustituyen las producciones de A por A-> β1A' | β2A' |... | βn A' A'->α1A' | a2 A'|... | αnA' | Є El no terminal A genera las mismas cadenas que antes, pero ya no es recursivo por la izquierda. Este procedimiento elimina toda la recursión inmediata por la izquierda de las producciones A y A' (suponiendo que ningún α1 es Є), pero no elimina la recursión por la izquierda que incluya derivaciones de dos o más pasos. Por ejemplo, considérese la gramática S-> Aα | b A-> Ac | Sd | Є El no terminal S es recursivo por la izquierda, porque S =>Aα =>Sdα, pero no es recursivo inmediato por la izquierda. |