2.4.1. Expresiones Regulares
|
En Pascal, un identificador es una letra seguida de cero o más letras o dígitos; es decir, un identificador es un miembro del conjunto de todas las cadenas de letras y dígitos que comienzan con una letra. Con esta notación, se pueden definir los identificadores de Pascal como letra ( letra | dígito ) * La barra vertical aquí significa "o", los paréntesis se usan para agrupar sub-expresiones, el asterisco significa "cero o más casos de" la expresión entre paréntesis, y la yuxtaposición de letra con el resto de la expresión significa concatenación. Una expresión regular se construye a partir de expresiones regulares más simples utilizando un conjunto de reglas definitorias. Cada expresión regular r representa un lenguaje L(r). Las reglas de definición especifican cómo se forma L(r) combinando de varias maneras los lenguajes representados por las subexpresiones de r. Las siguientes son las reglas que definen las expresiones regulares del alfabeto ∑. Asociada a cada regla hay una especificación del lenguaje representado por la expresión regular que se está definiendo.
Se dice que un lenguaje designado por una expresión regular es un conjunto regular. La especificación de una expresión regular es un ejemplo de definición recursiva. Las reglas 1 y 2 son la base de la definición; se usa el término símbolo básico para referirse a Є o a un símbolo de ∑ que aparezcan en una expresión regular. La regla 3 proporciona el paso inductivo. Se pueden evitar los paréntesis innecesarios en las expresiones regulares si se adoptan las convenciones:
Según estas convenciones, (a)| ((b)*(c)) es equivalente a a|b*c. Estas dos expresiones designan el conjunto de cadenas que tienen una sola a, o cero o más b seguidas de una c. |
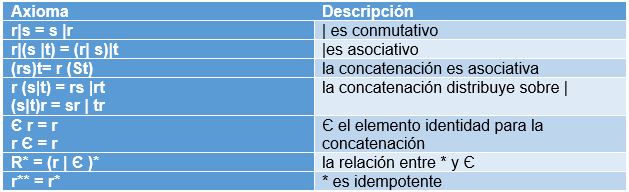 |
| Figura 1. Propiedades algebraicas de las expresiones regulares |