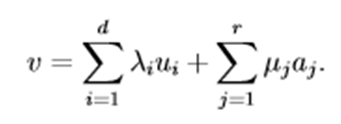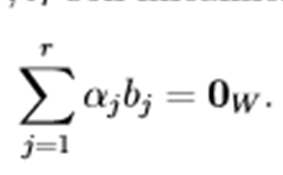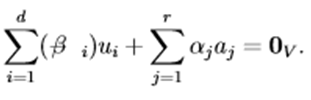Definición (rango de una transformación lineal). Sean V,W espacios vectoriales sobre un campo F y sea T ∈ L(V,W). El rango de T se define como la dimensión de la imagen de T: 

                                       r(T) = dim(im(T)).

Definición (nulidad de una transformación lineal). Sean V,W espacios vectoria- les sobre un campo F y sea T ∈ L(V,W). La nulidad de T se define como la dimensión del núcleo de T: 

                                       nul(T) = dim(ker(T)).

Teorema de la nulidad y el rango de una transformación lineal. Sean V y W espacios vectoriales sobre un campo F, dim(V ) < +∞, y sea T ∈ L(V,W). Entonces dim(im(T)) < +∞ y

                              nul(T) + r(T) = dim(V ), (1)

esto es,

                              dim(im(T)) + dim(ker(T)) = dim(V ).

Demostración. Sea u₁,...,u_d una base de ker(T). Los vectores u₁,...,u_d son linealmente independientes y el espacio V es de dimensión finita, por lo tanto existen vectores a₁,...,a_r ∈ V tales que la lista u₁,...,u_d,a₁,...,a_r es una base de V . Para todo j ∈ {1,...,r} pongamos bj = T(aj).

Vamos a demostrar que b1,...,br es una base de im(T). Con eso obtendremos la igualdad (1) porque d + r = dim(V ).

1. Mostremos que ℓ(b1,...,br) = im(T). Sea w ∈ im(T). Por la definición im(T), existe un v ∈ V tal que w = Tv. Escribamos v como una combinación lineal de los vectores u₁,...,u_d,a₁,...,a_r:

Aplicamos T al vector v tomando en cuenta la linealidad de T y el hecho que u₁,...,u_d ∈ ker(T):

2. Mostremos que los vectores b₁,...,b_r son linealmente independientes. Supongamos que

entonces

Pasamos todos los sumandos a un lado de la igualdad:

Los vectores u₁,...,u_d,a₁,...,ar forman una base de V y por lo tanto son linealmente independientes. Esto implica que todos los coeficientes βi y αj son 0. En particular,
                                                                   

                                                         α₁ = ... = α_r = 0.