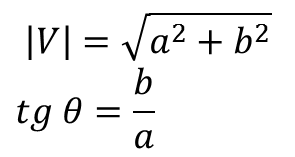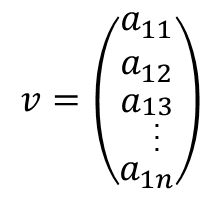5.1.- Estructura axiomática de espacio vectorial

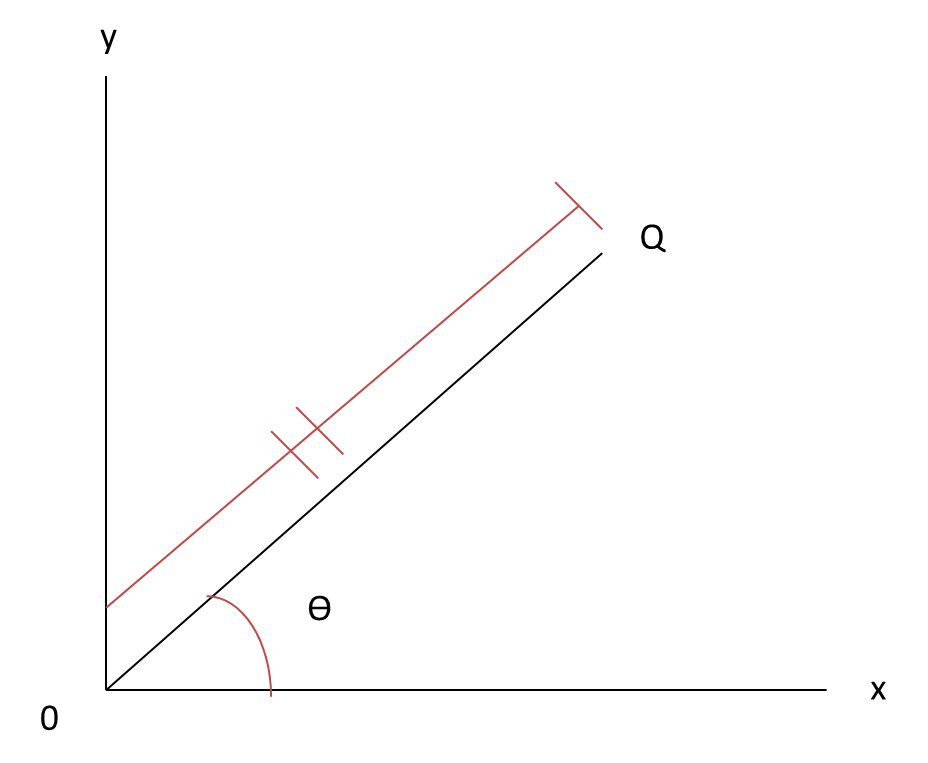
Para comenzar este tema se tiene que definir qué es un vector, y un vector es un segmento de recta dirigida de P a Q. Y su gráfica sería la siguiente:

Un vector posee magnitud y dirección

Algebraica: Es un conjunto de elementos ordenados en renglón o columna.

v= a11, a12, a13... a1n    

 

Ahora bien, un espacio vectorial responde a la suma y la multiplicación por un escalar:

1º

 

V1=(-1, -3)

V2=(-3, -9)

V3=(5, 15)

V1+V2=(-1, -12)

2º 

V1=(-2, 4)            V1+V2=(-7, 12)

V2=(-5, 8)            .·.No es un espacio vectorial

 

3º 

V1=(2, 1)              V1+V2=(7, 2)                .·.No es un espacio vectorial

V2=(5, 1)

 

4º 

V1=(8, 0)                     V1+V2=(10, 0)

V2=(2, 0)                                                  .·.Es un espacio vectorial

                                 

 

AXIOMAS DE UN ESPACIO VECTORIAL.

  1. Si x Є V y y Є V, entonces x + y Є V (Cerradura bajo la suma).
  2. Para todo x, y, z en V, (x + y) + z = x + (y + z)
    (Ley asociativa de la suma de vectores)
  1. Existe un vector 0 Є V tal que para todo x Є V, x + 0 = 0 + x = x
  2. Si x Є V, existe un vector –x en V tal que x + (–x) = 0
    (–x se llama inverso aditivo de x)
  3. Si x y y están en V, entonces x + y = y + x.
    (Ley conmutativa de la suma de vectores).
  1. Si x Є V y α es un escalar, entonces αx Є V
    (Cerradura bajo la multiplicación por un escalar).
  1. Si x y y están en V y α es un escalar, entonces α(x + y) = αx + αy

(Primer ley distributiva)

  1. Si x Є V y α y β son escalares, entonces (α + β)x = αx + βx

(Segunda ley distributiva)

  1. Si x Є V y α y β son escalares, entonces α(βx) = (αβ)x

(Ley asociativa de la multiplicación por escalares)

  1. Para cada vector x Є V, 1x = x.