Base: Un conjunto finito de vectores  v₁, v₂, . . ., v_n  es una base para un espacio vectorial V si

i.  v₁, v₂, . . ., v_n   es linealmente independiente

ii. v₁, v₂, . . ., v_n   genera V.

Todo conjunto de n vectores linealmente independiente Rⁿ  es una base en Rⁿ

En Rⁿ   se define

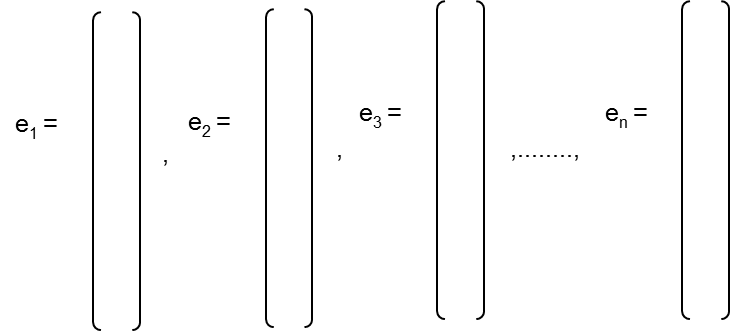
Base canónica.-  Entonces, como los vectores e₁ son las columnas de una matriz identidad e₁, e₂, . . ., e_n   es un conjunto linealmente independiente y, por lo tanto, constituye una base en Rⁿ.  

Ejemplo:

Demuestre que el conjunto  y   son bases para R^2.

Cualquier vector   se puede escribir como , entonces B₁ genera a R².Si (0,0)=(1, 0)+ β(0, 1) entonces (0,0)=(λ,β) luego λ=β=0 , por tanto B₁ es un conjunto L.I. lo que implica que como B₁ genera a R² y es L.I. entonces  B₁ es base para R² .

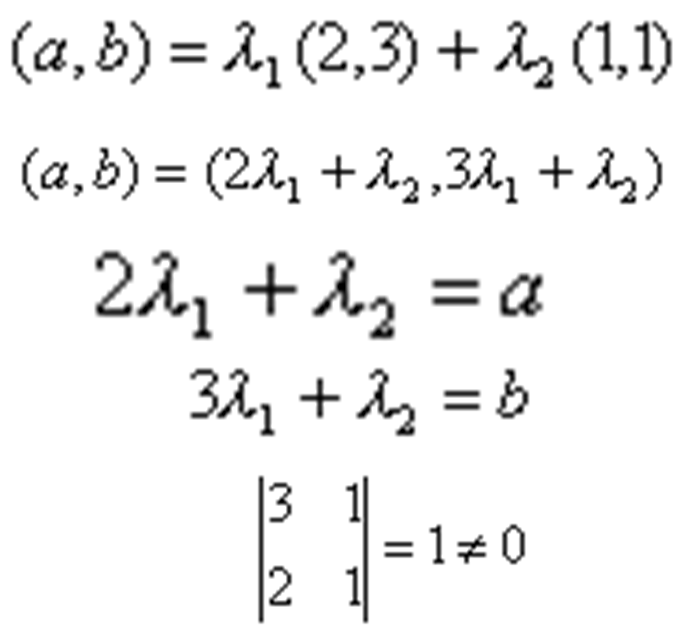
Debemos probar que para cualquier vector  , existen escalares  tales que