5.2.2.- Dependencia e independencia lineal.
|
Sea
Es
decir, son linealmente independientes cuando la única
manera de verificarse la igualdad Se
dice que los vectores
Ejemplo
1 En el espacio vectorial usual
Solución:
La igualdad
Sumando
a la primera ecuación la segunda multiplicada por
|
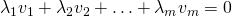 es para
es para 
 son linealmente
dependientes o bien que
son linealmente
dependientes o bien que 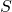 es un sistema
ligado si y sólo si no son linealmente
independientes. Es decir, cuando para algunos
es un sistema
ligado si y sólo si no son linealmente
independientes. Es decir, cuando para algunos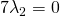 o bien,
o bien, 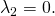 Sustituyendo
en la segunda deducimos
Sustituyendo
en la segunda deducimos 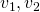 son
linealmente independientes.
son
linealmente independientes.