Combinación lineal entre vectores

El curso de álgebra lineal puede a la vez considerarse aburrido por monotemático; el problema fundamental
del álgebra lineal es resolver sistemas de ecuaciones lineales. Y por consiguiente, prácticamente la totalidad de los temas tiene como fin analizar los sistemas lineales y sus soluciones. Después del concepto de sistema de ecuaciones el segundo concepto en importancia es el de combinación lineal. Veamos cómo se motiva este concepto.

Ejemplo:

Supongamos el sistema de ecuaciones lineales:
                                x −  y = 1
                             2 x +  y = 5
Sabemos que cada ecuación representa una línea recta en R2 y que la solución a él coincide con la intersección de las rectas.

Para buscar otra visión de la situación, sustituimos la solución x = 2   y    y= 1:
                                1 (2) + (−1)(1) = 1
                                    2 (2) + 1(1) = 5
En notación vectorial, lo anterior queda

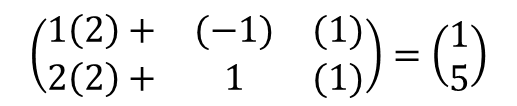
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por dos escalares.

Cualquier vector se puede poner como combinación lineal de otros que tengan distinta dirección.