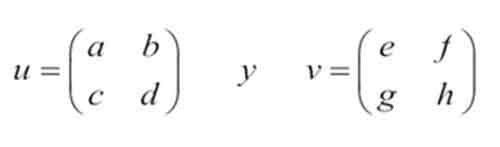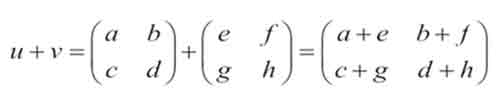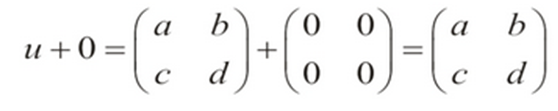Considere el conjunto de matrices reales de 2 x 2. Denote este conjunto como M₂₂. En la sección de matrices se definieron las operaciones de adición y multiplicación por un escalar en este conjunto y, de hecho, éste forma un espacio vectorial.

Se analizarán algunos axiomas para comprobar esto.
Utilizando la notación vectorial para indicar los elementos de M₂₂, sean:

dos matrices de 2 x 2 cualesquiera. Se tiene entonces que:

Axioma 1:

u + v es una matriz de 2 x 2. Por consiguiente, M₂₂ es cerrada bajo la adición.

Axiomas 2

De acuerdo al tema anterior de matrices, se sabe que las matrices de 2 x 2 son conmutativas y asociativas bajo la adición.

Axioma 3:

La matriz cero de 2 x 2 es 0=, puesto que

Axioma 4:

Si , entonces  ya que 

El conjunto de matrices M₂₂ de 2 x 2 constituye un espacio vectorial. Las propiedades algebraicas de M₂₂ son similares a las de Rⁿ . Asimismo, se puede concluir que M_mn, el conjunto de matrices de m x n es un espacio vectorial.